Đáp án A.

Chọn B

Phương pháp:

Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.

Ta sử dụng phương trình  có hai nghiệm dương phân biệt 

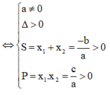
Cách giải:

Ta có 

Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.

Khi đó 

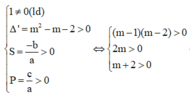
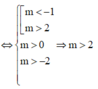
Mà  nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

BBT:

Chọn đáp án C.

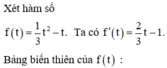
Bình luận:

Quay lại với lời giải ở trên: Ta chia cả 2 vế của (*) cho x chính là chia cả 2 vế của (2) cho  

Đáp án A

Để hàm số đồng biến trên khoảng 2 ; + ∞ thì

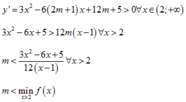
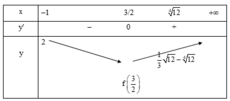
Xét f x = 3 x 2 − 6 x + 5 12 x − 1 có đạo hàm  f ' x = 3 x 2 − 6 x + 1 12 x − 1 2 > 0 x > 2

Do đó f(x) đồng biến trên khoảng 2 ; + ∞  hay  M i n f x = f 2 = 5 12 ⇒ m < 5 12

Lại có m ∈ − 2017 ; 2017 m ∈ ℤ .

Suy ra có 2018 giá trị của m thỏa mãn

Chọn: D

PT:  x 2 - 4 x - 5 - m = 0 ⇔ x 2 - 4 x - 5 = m 1

Số nghiệm phương trình (1) bằng số giao điểm của đồ thị hàm số 

y = x 2 - 4 x - 5 P  và đường thẳng y = m (cùng phương Ox)

Xét hàm số  y = x 2 - 4 x - 5 P 1  có đồ thị như hình 1.

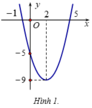
Xét hàm số  y = x 2 - 4 x - 5 P 2  là hàm số chẵn nên có đồ thị nhận Oy làm trục đối xứng.

Mà  y = x 2 - 4 x - 5 = x 2 - 4 x - 5  nếu  x ≥ 0

Suy ra đồ thị hàm số  P 2  gồm hai phần:

Phần 1: Giữ nguyên đồ thị hàm số  P 1  phần bên phải Oy.

Phần 2: Lấy đối xứng phần 1 qua trục Oy.

Ta được đồ thị  P 2  như hình 2.

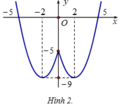
Xét hàm số  y = x 2 - 4 x - 5 P , ta có:  x 2 − 4 x − 5     ( y ≥ 0 ) − x 2 − 4 x − 5     ( y < 0 )

Suy ra đồ thị hàm số (P) gồm hai phần:

Phần 1: Giữ nguyên đồ thị hàm số  P 2  phần trên Ox.

Phần 2: Lấy đối xứng đồ thị hàm số  P 2  phần dưới Ox qua trục Ox.

Ta được đồ thị (P) như hình 3.

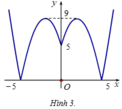
Quan sát đồ thị hàm số (P) ta có:

Phương trình |x² – 4 |x| − 5| − m = 0 (1) có hai nghiệm phân biệt  ⇔ m > 9 m = 0

Mà  m ∈ Z m ∈ 0 ; 2017 ⇒ m ∈ 0 ; 10 ; 11 ; 12 ; . . . ; 2017

Vậy có 2009 giá trị nguyên của m thỏa mãn.

Đáp án cần chọn là: C

Hàm số  y = ln x 2 - 2 x - m + 1  xác định trên R

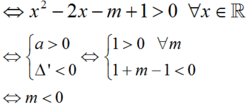
Mà

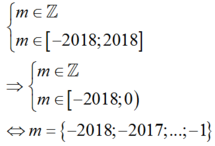
Vậy có 2018 giá trị của m thỏa mãn yêu cầu bài toán.

Chọn A.