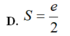Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f x trục hoành và hai đường thẳng x = a và x = b a < b được tính theo công thức nào dưới đây ?
A. S = ∫ a b f x d x
B. S = π ∫ a b f 2 x d x
C. S = π ∫ a b f x d x
D. S = ∫ a b f x d x
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
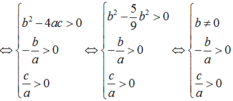
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
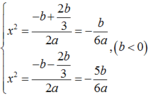
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
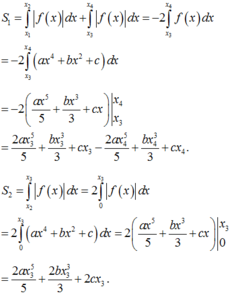
Suy ra
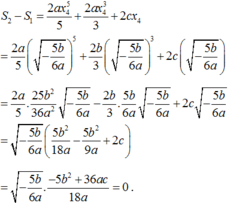
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
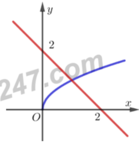
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Biết đồ thị hàm số f x = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f(x) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2
B. S 1 S 2 = 1 4
C. S 1 S 2 = 1 2
D. S 1 S 2 = 1
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f(x) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
⇔ b 2 − 4 a c > 0 − b a > 0 c a > 0 ⇔ b 2 − 5 9 b 2 > 0 − b a > 0 c a > 0 ⇔ b ≠ 0 − b a > 0 c a > 0
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a>0.
Khi đó x 2 = − b + 2 b 3 2 a = − b 6 a x 2 = − b − 2 b 3 2 a = − 5 b 6 a , b < 0 .
Suy ra
x 1 = − − 5 b 6 a ; x 2 = − − b 6 a ; x 3 = − b 6 a ; x 4 = − 5 b 6 a
Do đồ thị hàm số f(x) nhận trục tung làm trục đối xứng nên ta có:
S 1 = ∫ x 1 x 2 f x d x + ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 f x d x = − 2 ∫ x 3 x 4 a x 4 + b x 2 + c d x
= − 2 a x 5 5 + b x 3 3 + c x x 4 x 3 = 2 a x 3 5 5 + b x 3 3 3 + c x 3 − 2 a x 4 5 5 + b x 4 3 3 + c x 4 .
S 2 = ∫ x 2 x 3 f x d x = 2 ∫ 0 x 3 f x d x = 2 ∫ 0 x 3 a x 4 + b x 2 + c d x = 2 a x 5 5 + b x 3 3 + c x x 3 0
= 2 a x 3 5 5 + 2 b x 3 3 3 + 2 c x 3 .
Suy ra
S 2 − S 1 = 2 a x 4 5 5 + 2 a x 4 3 3 + 2 c x 4 = 2 a 5 − 5 b 6 a 5 + 2 b 3 − 5 b 6 a 3 + 2 c − 5 b 6 a
= 2 a 5 . 25 b 2 36 a 2 − 5 b 6 a − 2 b 3 . 5 b 6 a − 5 b 6 a + 2 c − 5 b 6 a = − 5 b 6 a 5 b 2 18 a − 5 b 2 9 a + 2 c
= − 5 b 6 a . − 5 b 2 + 36 a c 18 a = 0
Vậy S 1 = S 2 hay S 1 S 2 = 1 .
Cho hàm số y= f( x) =ax4+ bx2+ c ( a> 0) có đồ thị (C), đồ thị hàm số y= f’(x). Đồ thị hàm số y= f( x) tiếp xúc với trục hoành tại hai điểm. Tính diện tích của hình phẳng giới hạn bởi đồ thị (C) và trục hoành?
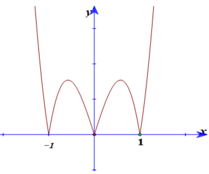
A. 7 15
B. 8 15
C. 14 15
D. 16 15
+ Từ đồ thị của hàm số và a> 0 ta dễ dàng có được đồ thị hàm số y= f’(x) như sau:
Ta có : f’(x) = 4ax3+ 2bx
Đồ thị hàm số y= f’(x) đi qua 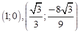 ta tìm được a=1 và b= -2
ta tìm được a=1 và b= -2
Suy ra hàm số đã cho có dạng: f(x) =x4-2x2+d và f’(x) = 4x3-4x.
+ Do (C) tiếp xúc với trục hoành nên f’(x) = 0 khi x=0; x=1; x=- 1.
Do (C) đối xứng qua trục tung nên (C) tiếp xúc với trục hoành tại 2 điểm (1; 0) và (-1; 0).
Do đó: f(0) =1 suy ra 1= 0-2.0+ d nên d= 1
Vậy hàm số cần tìm là: y =x4-2x2+1
+ Xét phương trình hoành độ giao điểm của (C) với trục hoành:
x4-2x2+1 =0 nên x=± 1
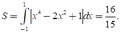
Chọn D.
Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x)=x(x-1)(x-2) và trục hoành bằng
A. ∫ 0 2 f ( x ) dx
B. ∫ 0 2 f ( x ) dx
C. ∫ 1 2 f ( x ) dx - ∫ 0 1 f ( x ) dx
D. ∫ 0 1 f ( x ) dx - ∫ 1 2 f ( x ) dx
Cho hàm số y = f(x) liên tục trên [a, b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức
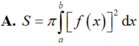
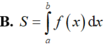
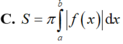

Chọn D
Hàm số y = f(x) liên tục trên [a; b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a; x = b được tính theo công thức S = ∫ a b f x d x .
Cho hàm số y = f(x) liên tục trên [a;b] Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y=f(x) trục hoành và hai đường thẳng x=a; x=b được tình theo công thức.
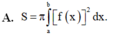
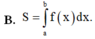
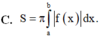
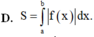
Cho hàm số y = f(x) liên tục trên [a;b]. Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x=a, x=b được tình theo công thức.
A. S = π ∫ a b f x 2 d x .
B. S = ∫ a b f x d x .
C. S = π ∫ a b f x d x .
D. S = ∫ a b f x d x .
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là:
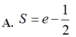
![]()
![]()