Thể tích khối vật thể tròn xoay khi quay hình phẳng (S) giới hạn bởi các đường y = 1 - x 2 , y = 0 quanh trục hoành có kết quả dạng π a b với a b là phân số tối giản. Khi đó a+b bằng:
A. 31
B. 23
C. 21
D. 32
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = ln x ; y = 0 ; x = 1 ; x = 2 quanh trục Ox là
A. V = πln 2
B. V = π ln 4 - 1
C. V = ln 4 + 1
D. V = π 2 - ln 4
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = x 2 ; y=0; x=1; x=2 quanh trục Ox là
A. 5 π 12
B. π 12
C. 7 π 12
D. 3 π 12
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = x 2 , y = 0 , x = 1 , x = 2 quanh trục Ox là
A. 5 π 12
B. 3 π 12
C. 7 π 12
D. π 12
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = lnx , y = 0, x = 1, x = 2 quanh trục Ox là
A. V = πln 2
B. V = π ln 4 − 1
C. V = ln 4 + 1
D. V = π 2 − ln 4
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = ln x , y = 0 , x = 2 quanh trục Ox là:
![]()
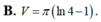
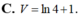
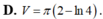
Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x 3 ; y=0; x=0; x=1 quanh trục hoành bằng

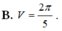
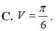
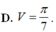
Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y = x 3 , y = 0 , x = 0 , x = 1 quanh trục hoành bằng
A. V = π 4
B. V = 2 π 5
C. V = π 6
D. V = π 7
Thể tích vật thể tròn xoay khi quay hình phẳng H giới hạn bởi các đường y = x 3 , y = 0 , x = 0 , x = 1 quanh trục hoành bằng
A. V = π 4
B. V = 2 π 5
C. V = π 6
D. V = π 7
Thể tích vật thể tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = x 1 2 . e x 2 , x=1, x=2, y=0 quanh trục Ox bằng
A. π e 2 + e
B. π e 2 - e
C. πe
D. πe 2
Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y = tanx, y = 0, x = 0, x = π 3 quanh Ox là:
A. 3 - π 3
B. π 3 - 3
C. π 2 3 - π 3
D. π 3 - π 2 3