Cho hàm số y = f(x) liên tục trên nửa khoảng − 2 ; 3 , có bảng biến thiên như hình vẽ
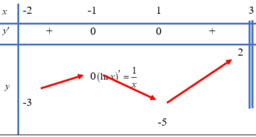
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số đạt cực tiểu tại x = -1
B. max − 2 ; 3 y = 2
C. min − 2 ; 3 y = − 3
D. Cực đại của hàm số bằng 0
Cho hàm số y = f ( x ) liên tục trên nửa khoảng [ - 3 ; 2 ) , có bảng biến thiên như hình vẽ
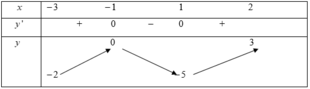
A. m a x [ - 3 ; 2 ] y = 3
B. m i n [ - 3 ; 2 ] y = - 2
C. Giá trị cực tiểu của hàm số là 1.
D. Hàm số đạt cực đại tại x = - 1
Đáp án là D.
Từ BBT ta thấy hàm số đạt cực đại tại x = - 1
Cho hàm số y=f(x) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
|
|
|
||
|
|
+ |
||
|
|
3 |
||
A.Không tồn tại giá trị nhỏ nhất của hàm số ![]()
B.Hàm số nghịch biến trên khoảng ![]()
C. ![]()
D. Đường thẳng ![]() là tiệm cận đứng của đồ thị hàm số
là tiệm cận đứng của đồ thị hàm số ![]()
Cho hàm số y = f(x) có f’ (x) liên tục trên nửa khoảng [0;+∞) thỏa mãn biết 3f(x) + f(x) = 1 + 3 e - 2 x . Giá trị f(0) = 11 3 . Giá trị f 1 2 ln 6 bằng
A. 1 2
B. 5 6 18
C. 1
D. 5 6 9
Đáp án B
Phương pháp: Đạo hàm: ![]()
Cách giải:

![]()
![]()

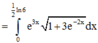
Ta có:
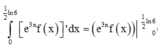

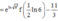
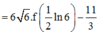


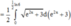
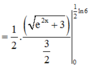
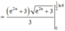
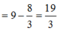
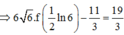
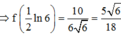
Cho hàm số y = f(x) có đạo hàm liên tục trên i. Đồ thị hàm số y = f’(x) như hình bên dưới
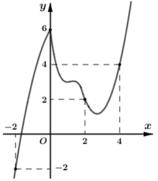
Hàm số g(x) = 2 f(x) - x 2 đồng biến trên khoảng nào trong các khoảng sau đây?
![]()
![]()
![]()
![]()
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Đồ thị hàm số y= f’(x) như hình bên dưới
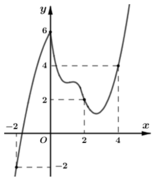
Hàm số g(x) = 2 . f(x) – x2 đồng biến trên khoảng nào trong các khoảng sau đây?
A. ( - ∞ ; - 2 )
B. (-2; 2)
C. (2; 4)
D. ( 2 ; + ∞ )
Cho hàm số y=f(x) liên tục trên đoạn [1;4] và có đồ thị hàm số y=f'(x) như hình bên. Hỏi hàm số g(x)=f( x 2 + 2 ) nghịch biến trên khoảng nào trong các khoảng sau?
![]()
![]()
![]()
![]()
Cho hàm số y=f(X) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình dưới. Khẳng định nào sau đây là sai?
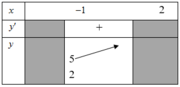
A. Hàm số đồng biến trên khoảng (0;1)
B. Đồ thị hàm số không đi qua điểm M(2;5)
C. m i n y = 2 [ - 1 ; 2 )
D. m a x y = 5 [ - 1 ; 2 )
Cho hàm số y=f(x) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình dưới. Khẳng định nào sau đây là sai?
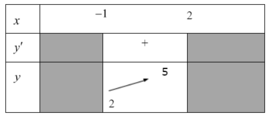
A.Hàm số đồng biến trên khoảng (0;1)
B. Đồ thị hàm số không đi qua điểm M(2;5)
C. ![]()
D. ![]()
Cho hàm số y = f ( x ) liên tục trên nửa khoảng [-1;2) có bảng biến thiên như hình vẽ. Khẳng định nào sau đây là đúng?
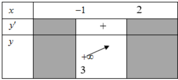
A. Không tồn tại giá trị nhỏ nhất của hàm số [-1;2)
B. Hàm số nghịch biến trên khoảng (-1;2)
C. Đường thẳng y = 0 là tiệm cận đứng của đồ thị hàm số y=f(x)
D. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số y=f(x)
Cho hàm số y=f(x) có đạo hàm liên tục trên ~ , hàm số y=f’(x) có đồ thị hàm số như hình dưới đây
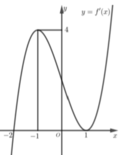
Hàm số y=f(x) đồng biến trên khoảng nào trong các khoảng sau:
A. (-∞;2); (1;+∞)
B. (-2;+∞)/{1}
C. (-2;+∞)
D. (-4;0)
Chọn C
Từ đồ thị hàm số y=f’(x) ta có bảng biến thiên cho hàm số y=f(x) như sau:
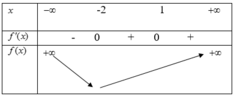
Nhìn vào bảng biến thiên ta thấy ngay trong khoảng (-2;+∞) thì hàm số y=f(x) đồng biến