Cho f(x) mà hàm số y = f’(x) có bảng biến thiên như hình vẽ bên. Tất cacr các giá trị của tham số m để bất phương trình m + x 2 < f x + 1 3 x 3 nghiệm đúng với mọi x ∈ 0 ; 3 là
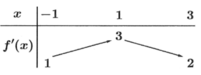
A. m < f(0)
B. m ≤ f 0
C. m ≤ f 3
D. m ≤ f 1 - 2 3
Cho f(x) mà hàm số y = f ' ( x ) có bảng biến thiên như hình bên. Tất cả các giá trị của tham số m để bất phương trình m + x 2 < f x + 1 3 x 3 nghiệm đúng với mọi x ∈ 0 ; 3 là
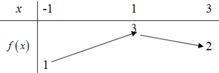
A. m < f 0
B. m ≤ f 0
C. m ≤ f 3
D. m < f 1 - 2 3
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
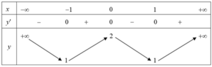
Tìm tất cả các giá trị thực của tham số m để phương trình f(x) - m =0 có 4 nghiệm phân biệt.
A. m ∈ ( 1 ; 2 ]
B. m ∈ [ 1 ; 2 )
C. m ∈ ( 1 ; 2 )
D. m ∈ [ 1 ; 2 ]
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ sau.
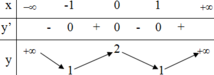
Tìm tất cả các giá trị thực của tham số m để phương trình f(x)-m=0 có 4 nghiệm phân biệt.
A. m ϵ (1 ;2]
B. m ϵ [1 ;2)
C. m ϵ (1 ;2)
D. m ϵ[1 ;2)
Từ bảng biến thiên ta dễ có 1 <m <2
Chọn đáp án C.
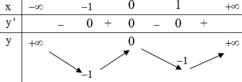
Cho hàm số y=f(x) xác định trên R\{0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình vẽ sau:
Tìm tất cả các giá trị của tham số thực m để phương trình f(x) -m=0
A. m ∈ 3 ; + ∞
B. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
C. m ∈ 3 ; + ∞
D. m ∈ − ∞ ; 1 ∪ 3 ; + ∞
Đáp án A.
Ta có f x − m = 0 ⇔ f x = m . Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = m .Do đó để phương trình đã cho có nghiệm duy nhất thì đường thẳng y = m phải cắt đồ thị hàm số y = f x tại một điểm duy nhất. Khi đó m ∈ 3 ; + ∞ .
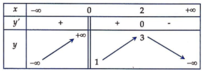
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ:
Tìm tất cả các giá trị của để phương trình f(x)=m có 3 nghiệm phân biệt
A. − 2 < m < 1
B. − 2 < m
C. − 2 ≤ m < 1
D. − 2 ≤ m ≤ 1
Đáp án A
Để phương trình f(x)=m có 3 nghiệm phân biệt thì đường thẳng y=m cắt đồ thị hàm số tại 3 điểm phân biệt.
Dựa vào bảng biến thiên ta thấy -2<m<1
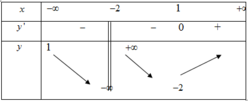
Cho hàm số y = f(x) có bảng biến thiên như sau
Tìm tất cả các giá trị của tham số m để phương trình f(x) = 2m có nhiều nhất 2 nghiệm.
A. m ∈ − ∞ ; − 1 2 ∪ 0 ; + ∞
B. m ∈ 0 ; + ∞ ∪ − 1
C. m ∈ − ∞ ; − 1 ∪ 0 ; + ∞
D. m ∈ 0 ; + ∞ ∪ − 1 2
Đáp án A
Phương pháp giải:
Phương trình có nhiều nhất n nghiệm thì xảy ra các trường hợp có n nghiệm, có n – 1 nghiệm, … , vô nghiệm, dựa vào bảng biến thiên để biện luận số giao điểm của hai đồ thị hàm số
Lời giải:

Cho hàm số y=f(x) có bảng biến thiên như sau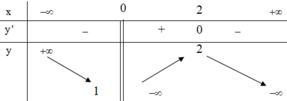
Tập hợp tất cả các giá trị của tham số m để phương trình f(x)+m=0 có 2 nghiệm phân biệt là
A. (-2;1)
B. [-1;2)
C. (-1;2)
D. (-2;1]
Cho hàm số y=f(x) có bảng biến thiên như sau
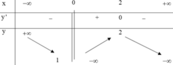
Tập hợp tất cả các giá trị của tham số m để phương trình f(x) + m =0 có 2 nghiệm phân biệt là
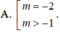
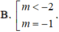
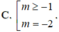
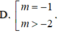
Cho hàm số y = f ( x ) có bảng biến thiên như sau:
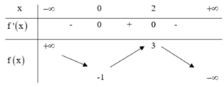
Tìm tất cả các giá trị của tham số m để phương trình f(x) = m có ba nghiệm thực phân biệt.
A. m ∈ (-1;+∞)
B. m ∈ (-∞;3)
C. m ∈ (-1;3)
D. m ∈ [-1;3]
Đáp án C
Phương pháp:
Số nghiệm của phương trình f(x) = m bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
Cách giải:
Số nghiệm của phương trình f(x) = m(*) bằng số giao điểm của đồ thị hàm số y = f(x) và đường thẳng y = m
⇒ Để (*) có 3 nghiệm thực phân biệt thì m ∈ (-1;3)