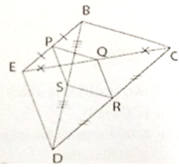
a) Ta có PS là đường trung bình của

Suy ra PS // AD và PS = AD/2

Để PQRS là hình chữ nhật ⇔ PQ ⊥ PS ⇔ BC ⊥ AD

Vậy tứ giác ABCD phải thêm điều kiện BC ⊥ AD thì PQRS là hình chữ nhật.

a)

Gọi H là trung điểm của AB

Tam giác ANB có S là trung điểm AN và H là trung điển AB

suy ra SH là đường trung bình tam giác ANB

suy ra HS song song với NB (1)

chứng minh tương tự ta có PH là đường trung bình của tam giác ABM

suy ra PH song song với AM (2)

ta co AM song song với NB (góc MAB=NBC= 60 độ)

(1) (2)suy ra P, S, H thẳng hàng 

ta có góc PHB=MAB=60 độ (đồng vị PH song songAM)

tam giác ANB có S là trung điểm AN và R là trung điểm NB

suy ra SR là đường trung bình tam giác ANB 

chúng minh tương tự ta gọi K là trung điểm BC

RK, QK là đường trung bình tam giác NBC, MBC

suy ra RK song song NC 

          QK song song MB

mà NC song song MB (góc MBA=NCB=60 độ đồng vị)

suy ra SR song song AB

suy ta góc PHB= PSR=60 độ(đồng vị  SR song song AB )

suy ra Q,R,K thẳng hàng 

ta có góc RKB= NBC=60 độ ( đồng vị RK song songNC)

suy ra góc RKB=QRS=60 độ (đông vị SR song song AB)

suy ra tứ giác PQRS có góc PSR= QRS=60 độ (3)

tam giác MBC có P trung điểm MB và Q trung điểm MC

suy ra PQ là đường trung bình tam giác MBC

suy ra PQsong song BC hay AC

chứng minh tương tự có SR là đường trung bình tam giác NAB

suy ra SR song song AB hay AC

suy ra PQ song song SR vậy PQRS là hình thang(3)

(3)(4)suy ra PQRS là hinh thang cân

b)tam giác MNB có P trung điểm MB và R trung điểm NB

suy ra PR là đường trung bình tam giác MNB

suy ra PR=1/2MN

mà PR=QS(PQRS là hình thang cân)

suy ra QS=1/2MN

cho xOy có tia phân giác là Oz . Trên tia Ox lấy 2 điểm A,B sao choA thuộc đoạn OB, C thuộc đoạn OD và AB=CD. Gọi M,N lần lượt là trung điểm của Ac, BD. Chứng minh MN sông song Với OZ

cũng chỉ vì mỏi tay nên được 69%

Do ∆ACM và ∆MDB đều => AC = AM = AC và MD = BD = MB. Nối M -> E; E -> F; F -> M 
Xét ∆AMD và ∆CMB có: 
+ AM = CM 
+ góc AMD = góc CMB = 120º (kề bù với 2 góc 60º) 
+ MD = MB 
=> ∆AMD = ∆CMB(c.g.c) => AD = BC => AD/2 = BC/2 => AE = CF và góc DAM = góc BCM 
Xét ∆AEM và ∆CFM có: 
+ AE = CF 
+ góc EAM = góc FCM 
+ AM = CM 
=> ∆AEM = ∆CFM(c.g.c) => EM = MF và góc AME = góc FMC 
=> góc AME + góc EMC = góc FMC + góc EMC 
=> góc MEF = góc AMC = 60º 
Xét ∆EFM có EM = MF và góc MEF = 60º => ∆EFM là tam giác cân có 1 góc = 60º 
=> ∆EFM là tam giác đều. 

B2) Lấy D ∈ AE sao cho AD = AC => DE = AB và ∆DAC đều 
Xét ∆ABC và ∆DEC có: 
+ AB = DE 
+ góc BAC = góc EDC = 120º (bạn tự chứng minh) 
+ AD = DC 
=> ∆ABC = ∆DEC(c.g.c) => BC = EC và góc ACB = góc DCE 
=> góc ACB + góc BCD = góc DCE + góc BCD 
=> góc ECB = góc ACD = 60º 
Xét ∆BEC có BC = EC và góc ECB = 60º => ∆BEC là tam giác cân có 1 góc = 60º 
=> ∆BEC là tam giác đều. 

B3) Do ∆ABC vuông cân tại A, có trung tuyên AM => AM cũng là phân giác, trung tuyến, đường cao,... 
=> BM = CM ;góc BAM = góc CAM = 45º => AM = MC(∆AMC vuông cân tại M) 
Xét ∆HAB và ∆KCA có: 
+ góc BHA = góc CKA = 90º 
+ AB = AC 
+ góc BAH = góc ACK (= 90º - góc CAK - bạn tự chứng minh) 
=> ∆HAB = ∆KCA(g.c.g) => AH = CK 
Ta có: góc HAB = góc ACK => góc HAB + góc BAM = góc ACK + góc MCA (do góc MAB = góc MCA = 45º) => góc MAH = góc MCK 
Xét ∆HAM và ∆KCM có 
+ AH = CK 
+ góc MAH = góc MCK 
+ AM = MC 
=> ∆HAM = ∆KCM (c.g.c) => HM = MK(1) và góc HMA = góc CMK 
=> góc HMA + góc AMK = góc CMK + góc AMK 
=> góc HMK = góc AMC = 90º (2) 
từ (1) và (2) => ∆HMK vuông cân tại M 
Cố hiểu nha bạn, có lẽ không tránh khỏi sai sót, nếu sai chỗ nào bạn cố hiều hộ mình, cố suy luận một chút vì bài dài quá!

a. chiều dài gấp đôi chiều rộng => CD=4x2=8(cm)

=> vẽ HCN có CD 8cm, CR 4 cm:

b. vẽ 1 đoạn thẳng chia HCN thành 2 HV sao cho cạnh HV là 4cm

c. chu vi HCN:

(8+4)x2=24(cm)

diện tích HCN:

8x4=32(cm²)

d. vì HCN gấp 2 lần HV nên CV và S HCN gấp 2 lần CV và S HV

duyệt cái gì nhanh zữ?!!!! lẹ lên giùm đi -_-

1. AB // CD (ABCD là hình thang) => ^B + ^D = 180^o (Trong cùng phía)

Mà ^B = ^A (ABCD là hình thang)  =>  ^A + ^D = 180^o

Xét hình thang ABCD có: ^A đối diện với ^D

 ^A + ^D = 180^o (cmt)

=> hình thang ABCD nội tiếp đường tròn

2. Xét hình chữ nhật LMNO có:

^L + ^N = 180^o (^L = 90^o; ^N = 90^o)

=> hình chữ nhật LMNO  nội tiếp đường tròn

3. Xét hình vuông PQRS có:

^P + ^R = 180^o (^P = 90^o; ^R = 90^o)

=> hình vuông PQRS nội tiếp đường tròn