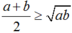Với α là số thực bất kỳ, mệnh đề nào sau đây là sai?
A. 10 α = 10 α 2
B. 10 α 2 = 100 α
C. 10 α = 1 0 α
D. 10 α 2 = 10 α 2
Với α là số thực bất kỳ, mệnh đề nào sau đây sai?
A. 10 α 2 = 100 α
B. 10 α = 10 α
C. 10 α = 10 α 2
D. 10 α 2 = 10 α 2
Với α là số thực bất kỳ, mệnh đề nào sau đây sai?
![]()
![]()
![]()
![]()
Với α là số thực bất kỳ, mệnh đề nào sau đây Sai?
A. 10 α = 10 α 2
B. ( 10 α ) 2 = 100 α
C. ( 10 α ) 2 = 10 α 2
D. 10 α = ( 10 ) β
Với α là số thực bất kỳ, mệnh đề nào sau đây sai
A. 10 α 2 = 100 α
B. 10 α = 10 α
C. 10 = 10 α 2
D. 10 α 2 = 10 α 2
Đáp án sai là D. Vì 10 α 2 = 10 2 α
Chọn đáp án D.
Giả sử f x là một hàm số bất kỳ liên tục trên khoảng α ; β và a , b , c , b + c ∈ α ; β . Mệnh đề nào sau đây sai?
A. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x
B. ∫ a b f x d x = ∫ a b + c f x d x - ∫ c b f x d x
C. ∫ a b f x d x = ∫ a c f x d x + ∫ b + c b f x d x
D. ∫ a b f x d x = ∫ a c f x d x - ∫ b c f x d x
+) Đáp án A:
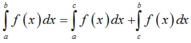
đáp án A đúng.
+) Đáp án C:
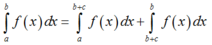
đáp án C đúng.
+) Đáp án D:
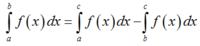
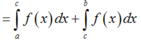
đáp án D đúng.
Chọn B.
Giả sử f(x) là một hàm số bất kỳ liên tục trên khoảng α ; β và a , b , c , b + c ∈ α ; β . Mệnh đề nào sau đây sai?
A. ∫ a b f x d x = ∫ a c f x d x + ∫ c b f x d x
B. ∫ a b f x d x = ∫ a b + c f x d x - ∫ a c f x d x
C. ∫ a b f x d x = ∫ a b + c f x d x + ∫ b + c b f x d x
D. ∫ a b f x d x = ∫ a c f x d x - ∫ b c f x d x
Với a, b, c là các số thực dương, a và c khác 1 và α ≠ 0. Mệnh đề nào dưới đây sai?
A. log a b . log c a = log c b
B. log a α b = α log a b
C. log a b c = log a b - log a c
D. log a b c = log a b + log a c
Đáp án B
Phương pháp:
Sử dụng các công thức liên quan đến logarit.
Cách giải:
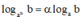 : là mệnh đề sai.
: là mệnh đề sai.
![]()
Cho a, b là các số thực dương, a ≠ 1 và α ∈ R . Mệnh đề nào sau đây đúng?
A. log a α b = log a b α .
B. log a α b = log a b α .
C. log a α b = 1 α l o g a b .
D. log a α b = log a α b .
Sử dụng bất đẳng thức để viết các mệnh đề sau
a) x là số dương.
b) y là số không âm.
c) Với mọi số thực α, |α| là số không âm.
d) Trung bình cộng của hai số dương a và b không nhỏ hơn trung bình nhân của chúng.
a) x > 0
b) y ≥ 0
c) ∀α ∈ R, |α| ≥ 0
d) ∀a, b > 0,