Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường y   =   x 3 ; y=0; x=0; x=1 quanh trục hoành bằng

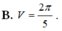
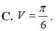
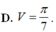
Thể tích vật thể tròn xoay khi quay hình phẳng (H) giới hạn bởi các đường  y = x 3 , y = 0 , x = 0 , x = 1 quanh trục hoành bằng

A. V =  π 4

B. V =  2 π 5

C. V =  π 6

D. V =  π 7

Cho hình phẳng (H) giới hạn bởi các đường y = x + 2 , y = x + 2 , x = 1 . Tính thể tích V của vật thể tròn xoay khi quay hình (H) quanh trục hoành.

A.  V = 27 π 2

B.  V = 9 π 2

C.  V = 9 π

D.  V = 55 π 6

Cho hình phẳng (H) giới hạn bởi các đường y = x + 2 , y = x + 2 , x = 1 . Tính thể tích V của vật thể tròn xoay khi quay hình (H) quanh trục hoành

A.  V = 27 π 2

B.  V = 9 π 2

C.  V = 9 π

D.  V = 55 π 6  

Cho hình phẳng (H) giới hạn bởi các đường y   =   x + 2 , y   =   x + 2 ; x = 1 . Tính thể tích V của vật thể tròn xoay khi quay hình (H) quanh trục hoành.

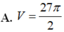
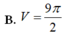
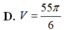
Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = xlnx; y = 0 ; x = 2 quay quanh trục Ox được tính bởi công thức nào?

A.  π ∫ 0 2 x 2 ln 2 xdx

B.  π ∫ 1 2 x 2 ln 2 xdx

C.  ∫ 0 2 x 2 ln 2 xdx

D.  ∫ 1 2 xlnxdx

Thể tích vật thể tròn xoay khi cho hình phẳng (H) giới hạn bởi các đường y = x ln x y = 0 ;   x = 2  quay quanh trục Ox được tính bởi công thức nào?

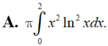
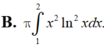
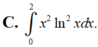
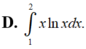
Trong mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường 4y = x² và y = x. Thể tích của vật thể tròn xoay khi quay hình (H) quanh trục hoành một vòng bằng

A.  128 30 π

B.  128 15 π

C.  32 15 π

D.  129 30 π

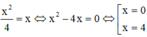
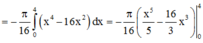
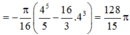
Tính thể tích V của vật tròn xoay tạo thành khi quay hình phẳng (H) giới hạn bởi các đường y = x 2 ; y = x  quanh trục Ox.

A.  V = 9 π 10 .

B.  V = 3 π 10 .

C.  V = π 10 .

D.  V = 7 π 10 .