Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số ( C m ) : y = x - 1 x 2 + x - m có hai đường tiệm cận đứng.
A. Mọi ![]()
B. 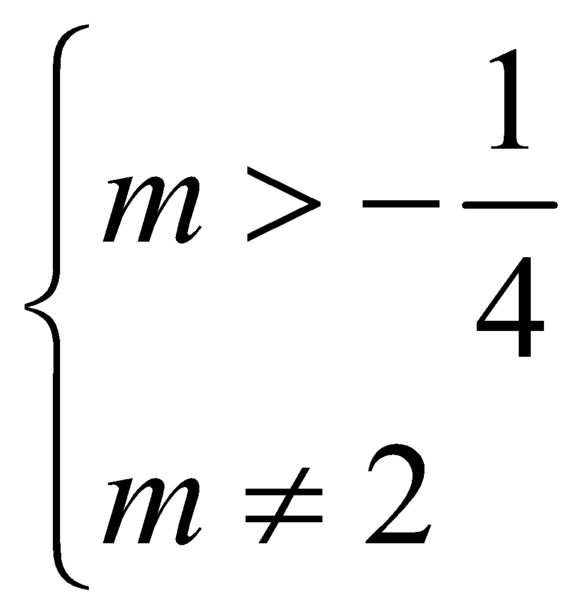
C. 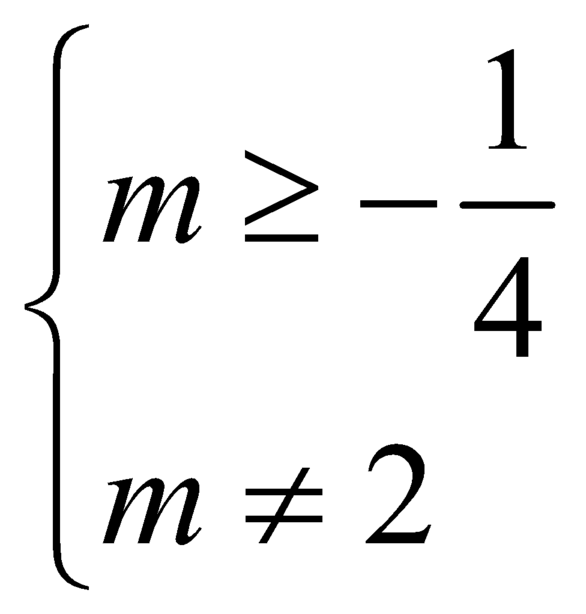
D. ![]()
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số có nghiệm sin 2 x + sin x cos x = m
A. − 1 4 ; 1 4
B. − 2 ; 2
C. 2 − 2 2 ; 2 + 2 2
D. 1 − 2 2 ; 1 + 2 2
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số sin 2 x + sin x . cos x = m có nghiệm
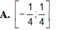
![]()
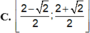
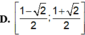
Tìm tất cả các giá trị của tham số thực m để đồ thị hàm số sin 2 x + sin x cos x = m có nghiệm
A. − 1 4 ; 1 4
B. − 2 ; 2
C. 2 − 2 2 ; 2 + 2 2
D. 1 − 2 2 ; 1 + 2 2
Đáp án D
Có m = 1 − cos 2 x 2 + 1 2 sin 2 x = 1 2 + 1 2 − cos 2 x + sin 2 x ⇔ − cos 2 x + sin 2 x = 2 m − 1
Điều kiện để phương trình có nghiệm là − 2 ≤ 2 m − 1 ≤ 2 ⇔ m ∈ 1 − 2 2 ; 1 + 2 2 .
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
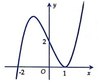
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > − 1
Cho hàm số y=f(x) có đồ thị như hình vẽ bên. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = f x + m có 5 điểm cực trị.
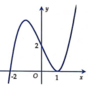
A. m ≤ − 1
B. m < − 1
C. m ≥ − 1
D. m > 1
Đáp án B.
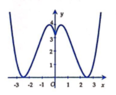
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x - 1 x - m có tiệm cận đứng.
A. Với mọi m
B. m ≠ 0
C. m ≠ 1
D. m = 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x − 1 x − m có tiệm cận đứng
A. m = 0
B. Với mọi m
C. m ≠ 1
D. m ≠ 0
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y = x x 2 − 2 x + m có một đường tiệm cận.
A. m=1
B. m=0
C. m ≤ 1
D. m>1
Đáp án D
Dễ thấy lim x → ∞ x x 2 − 2 x + m = 0 nên hàm số y = x x 2 − 2 x + m có tiệm có Δ < 0 . Khi đó Δ ' = 1 − m < 0 ⇒ m > 1.
Cho hàm số
y = 1 x 2 - 2 m + 1 x + 2 m x - m . Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số có 4 đường tiệm cận
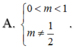
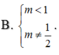
![]()
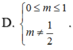
Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số y=sinx+cosx+mx đồng biến trên khoảng - ∞ ; + ∞
A . - 2 ≤ m ≤ 2
B . m ≤ - 2
C . - 2 < m < 2
D . m ≥ 2