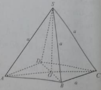
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a 6 , B A D ^ = 60 0 , cạnh bên SA vuông góc với đáy và SA = 3a. Số đo của góc giữa hai mặt phẳng (SBC) và (SCD) bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. 3
C. 3 2
D. Đáp án khác
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 120 0 .Cạnh bên S A = 3 a và SA vuông góc với (ABCD) .Tính a theo Vcủa khối chóp S.ABCD?
A. V = a 3 2
B. V = a 3 4
C. V = 3 a 3 4
D. V = 3 a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:
A. 1
B. 3
C. 3 2
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a , A B C ⏞ = 60 0 , cạnh bên SA vuông góc với đáy SA= a 3 Tính thể tích của khối chóp S.ABCD
A. a 3 4 .
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Đáp án là C.
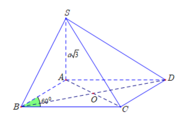
Ta có: S A B C = 1 2 B A . B C . sin A B C ⏞ = 1 2 a . a . sin 60 0 = a 2 3 4 ⇒ S A B C D = 2 S A B C = a 2 3 2 .
Thể tích của khối chóp S.BCD là:
V S . B C D = 1 3 S A . S B C D = 1 3 S A . 1 2 S A B C D = 1 3 . A = a 3 . a 2 3 2 = a 8 2 .
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Cạnh bên SA vuông góc với đáy (ABCD) và SA=3a. Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABCD
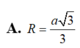
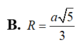
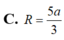
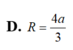
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, D ^ = 60° và SA vuông góc với (ABCD). Biết thể tích của khối chóp S.ABCD bằng a 3 2 . Tính khoảng cách k từ A đến mặt phẳng (SBC).
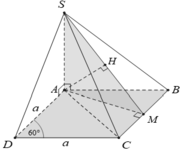
A. k = 3 a 5
B. k = a 3 5
C. k = 2 a 5
C. k = 2 a 5
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O có cạnh bằng a, góc BAC ^ = 60 ° , SO ⊥ ( ABCD ) và SO = 3a/4. Tính thể tích khối chóp S.ABCD.
A. a 3 3 8
B. a 3 3 4
C. a 3 4
D. 3 a 3 3 8
Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a có A B C ^ = 45 ° , ∆ SAD đều và (SAD) ⊥ (ABCD). Tính thể tích V của hình chóp.
A. V = a 3 2 6
B. V = a 3 6 12
C. V = a 3 3 8
D. V = a 3 4
cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, SA vuông góc với mặt phẳng đáy, SA=BD=a√3. Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) bằng
A. 60° B. 30° C.90° D.45°
Gọi O là giao điểm của AC và BD. Dễ thấy \(\Delta OAB\) vuông tại O và \(OB=\dfrac{a\sqrt{3}}{2}\). Từ đó \(OA=\sqrt{AB^2-OB^2}=\sqrt{\left(\dfrac{\sqrt{3}}{2}a\right)^2-a^2}=\sqrt{\dfrac{1}{4}a^2}=\dfrac{a}{2}\) \(\Rightarrow AC=a\).
Vì \(SA\perp mp\left(ABCD\right)\) nên \(SA\perp AC\) tại A hay \(\Delta SAC\) vuông tại A.
Lại có \(\tan SAC=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\) nên \(\widehat{SAC}=60^o\), suy ra góc giữa SC và mp(ABCD) bằng 60o \(\Rightarrow\) Chọn A
Chỗ \(\widehat{SAC}\) em sửa lại là \(\widehat{SCA}\) mới đúng ạ.
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a. Góc A bằng 60 o , O là tâm hình thoi, SA vuông góc với đáy. Góc giữa SO và mặt phẳng đáy bằng 45 o . Tính theo a thể tích khối chóp SABCD.
A. 3 2 a 3 x
B. a 3 4
C. 3 a 3 8
D. 2 a 3