Cho khối chóp S.ABC có S A ⊥ A B C , tam giác ABC đều cạnh a và tam giác SAB cân. Tính khoảng cách h từ điểm A đến mặt phẳng (SBC)
A. h = a 3 7 .
B. h = a 3 7 .
C. h = 2 a 7 .
D. h = a 3 2 .
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A
.
a
3
3
12
B
.
a
3
3
24...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, mặt phẳng (SAB) vuông góc với mặt phẳng (ABC) và tam giác SAB vuông cân tại S. Tính thể tích khối chóp S.ABC theo a
A . a 3 3 12
B . a 3 3 24
C . a 3 3 3
D . a 3 3 4
Đáp án B
Vì tam giác SAB cân tại S nên hạ SH ⊥ AB => H là trung điểm của AB.
Vì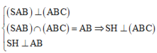 
Tam giác SAB vuông cân tại S nên SA = SB = a 2
Đúng 0
Bình luận (0)
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC A.
V
a
3
8
B.
V
a
3
3
3
C.
V
a
3...
Đọc tiếp
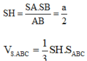
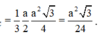
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Tính theo a thể tích khối chóp S.ABC
A. V = a 3 8
B. V = a 3 3 3
C. V = a 3 3 4
D. V = a 3 4
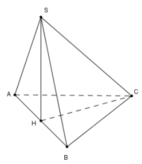
Vì SHlà đường trung tuyến trong tam giác SAB đều cạnh a nên
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a,
S
A
⊥
(
A
B
C
)
và
S
A
a
6
. Thể tích của khối chóp S.ABC bằng: A.
a
3
2
4
B.
a
3
2
C.
a...
Đọc tiếp
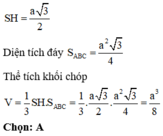
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, S A ⊥ ( A B C ) và S A = a 6 . Thể tích của khối chóp S.ABC bằng:
A. a 3 2 4
B. a 3 2
C. a 3 3 12
D. a 3 2 12
Đáp án A
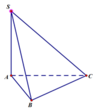
Do tam giác ABC đều cạnh a nên có S ∆ A B C = a 2 3 4
⇒ V = 1 3 S A . S ∆ A B C = 1 3 . a 6 . a 2 3 4 = a 2 2 4
Đúng 0
Bình luận (0)
cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với (ABC) tính thể tích khối chóp S.ABC.
cho hình chóp S.ABC có đáy ABC đều cạnh a, tam giác SBC cân tại S và nằm trong mặt phẳng vuông góc với (ABC) tính thể tích khối chóp S.ABC.
Ai đó giúp mk vứi thay câu hỏi thành tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác vuông tại A,
A
B
C
^
30
0
, SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là: A.
a
3
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, A B C ^ = 30 0 , SAB là tam giác đều cạnh a, hình chiếu vuông góc của S lên mặt phẳng (ABC) là trung điểm của cạnh AB. Thể tích của khối chóp S.ABC là:
A. a 3 3 9
B. a 3 18
C. a 3 3 3
D. a 3 12
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA
⊥
(ABC) và SA a
6
. Thể tích của khối chóp bằng:
A
.
a
3
2
4
B
.
a
3
2
C
.
a...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác đều cạnh a, SA ⊥ (ABC) và SA = a 6 . Thể tích của khối chóp bằng:
A . a 3 2 4
B . a 3 2
C . a 3 3 12
D . a 3 2 12
Đáp án A
Do tam giác ABC đều cạnh a nên có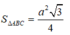 
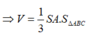
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA
⊥
(ABC) và SA
a
3
. Tính thể tích khối chóp S.ABC A.
2
a
3
3
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA ⊥ (ABC) và SA= a 3 . Tính thể tích khối chóp S.ABC
A. 2 a 3 3
B. a 3 2
C. a 3 4
D. 3 a 3 4
Chọn C.
Diện tích ∆ ABC là S A B C = a 2 3 4
SA ⊥ (ABC) nên SA là chiều cao của hình chóp và SA= a 3
Thể tích khối chóp là
V = 1 3 S A B C . S A = 1 3 . a 2 3 4 . a 3 = a 3 4
Đúng 1
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên
S
A
⊥
A
B
C
và
S
A
a
3
. Tính thể tích khối chóp S.ABC A.
a
3
3
B.
3
a
3
4
C. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên S A ⊥ A B C và S A = a 3 . Tính thể tích khối chóp S.ABC
A. a 3 3
B. 3 a 3 4
C. a 3 4
D. 2 a 3 3
Cho hình chóp S.ABC có SA 3a vuông góc với đáy và tam giác ABC là tam giác đều cạnh a. Tính thể tích V của khối chóp S.ABC. A. V
3
a
3
2
B. V
3
3
a
3
4
C. V
3...
Đọc tiếp
Cho hình chóp S.ABC có SA = 3a vuông góc với đáy và tam giác ABC là tam giác đều cạnh a. Tính thể tích V của khối chóp S.ABC.
A. V = 3 a 3 2
B. V = 3 3 a 3 4
C. V = 3 a 3 4
D. V = 3 3 a 3 2
Phương pháp:
Thể tích khối chóp V = 1 3 Sh với S là diện tích đáy, h là chiều cao.
Cách giải:
Tam giác ABC đều cạnh a nên diện tích 
Thể tích khối chóp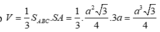 
Chọn: C
Đúng 0
Bình luận (0)