Cho A, B là hai điểm biểu diễn hình học của hai số phức z 1 , z 2 z 1 ≠ 0 , z 2 ≠ 0 và thỏa mãn z 1 2 + z 2 2 = z 1 z 2 . Hỏi ba điểm O, A, B tạo thành tam giác gì? (O là gốc tọa độ).
A. Tam giác đều
B. Cân tại O
C. Vuông tại O
D. Vuông cân tại O.
Những câu hỏi liên quan
Cho hai số phức z a + bi; a,b. Có điểm biểu diễn của số phức z nằm trong dải (-2;2) (hình 1) điều kiện của a và b là: A.
a
≥
2
b
≥
2...
Đọc tiếp
Cho hai số phức z = a + bi; a,b. Có điểm biểu diễn của số phức z nằm trong dải (-2;2) (hình 1) điều kiện của a và b là:
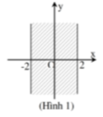
A. a ≥ 2 b ≥ 2
B. a ≤ - 2 b ≤ - 2
C. -2 < a < 2, b ∈ ℝ
D. a,b ∈ (-2;2)
Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn -2 < a < 2, b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
Đúng 0
Bình luận (0)
Cho hai số phức
z
a
+
bi
;
a
,
b
∈
ℝ
. Có điểm biểu diễn của số phức z nằm trong dải
−
2
;
2
(hình 1) điều kiện của a và b là: ...
Đọc tiếp
Cho hai số phức z = a + bi ; a , b ∈ ℝ . Có điểm biểu diễn của số phức z nằm trong dải − 2 ; 2 (hình 1) điều kiện của a và b là: a ≥ 2 b ≥ 2 a ≤ − 2 b ≤ − 2 − 2 < a < 2 , b ∈ ℝ a , b ∈ − 2 ; 2
A. a ≥ 2 b ≥ 2
B. a ≤ − 2 b ≤ − 2
C. − 2 < a < 2 , b ∈ ℝ
D. a , b ∈ − 2 ; 2
Đáp án C
- Nhìn vào hình vẽ ta có phần thực a bị giới hạn − 2 < a < 2 , b ∈ ℝ
Chú ý: Cho số phức z = a + bi, điểm M(a;b) trong hệ trục tọa độ vuông góc của mặt phẳng được gọi là điểm biểu diễn số phức z.
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
1
và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức
w
1
i
z
là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là A. Điểm M B. Điểm N C. Điểm P D. Điểm Q
Đọc tiếp
Cho số phức z thỏa mãn z = 1 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w = 1 i z là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là
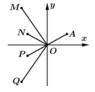
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
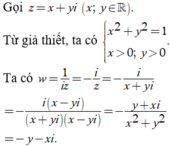
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-y;-x) (đều có hoành độ và tung độ âm). Đồng thời 
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn C.
Đúng 0
Bình luận (0)
Cho số phức z 2 + i.Hãy xác định điểm biểu diễn hình học của số phức
ω
(
1
-
i
)
z
. A. Điểm M B. Điểm N C. Điểm P D. Điểm Q
Đọc tiếp
Cho số phức z = 2 + i.
Hãy xác định điểm biểu diễn hình học của số phức ω = ( 1 - i ) z .
A. Điểm M
B. Điểm N
C. Điểm P
D. Điểm Q
Cho hai số phức w và z thỏa mãn
w
-
1
+
2
i
z
. Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r 3. Tìm tập hợp các điểm biểu diễn của số phức A. Là một đường thẳng song song trục tung B. Là một đường thẳng không song song với trục tung C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng
3
5...
Đọc tiếp
Cho hai số phức w và z thỏa mãn w - 1 + 2 i = z . Biết tập hợp các điểm biểu diễn của số phức z là đường tròn tâm I(-2;3) bán kính r = 3. Tìm tập hợp các điểm biểu diễn của số phức
A. Là một đường thẳng song song trục tung
B. Là một đường thẳng không song song với trục tung
C. Là đường tròn, tọa độ tâm (-3;5) bán kính bằng 3 5
D. Là đường tròn, tọa độ tâm (-1;1) bán kính bằng 3
Ta có : w - 1 + 2 i = z ⇔ w = z + 1 - 2 i . Suy ra quỹ tích các điểm biểu diễn số phức w có được từ quỹ tích các điểm biểu diễn số phức z bằng cách thực hiện phép tịnh tiến theo v → = ( 1 ; - 2 ) . Do đó quỹ tích quỹ tích các điểm biểu diễn số phức w là đường tròn tâm (-1;1) bán kính bằng 3.
Đáp án D
Đúng 0
Bình luận (0)
Cho số phức
z
6
+
7
i
.
Số phức liên hợp của z có điểm biểu diễn hình học là A. (-6;-7) B. (6;7) C. (6;-7) D. (-6;7)
Đọc tiếp
Cho số phức z = 6 + 7 i . Số phức liên hợp của z có điểm biểu diễn hình học là
A. (-6;-7)
B. (6;7)
C. (6;-7)
D. (-6;7)
Cho số phức z = 6 + 7 i . Số phức liên hợp của z có điểm biểu diễn hình học là
A. (-6;-7)
B. (6;7)
C. (6;-7)
D. (-6;7)
Cho số phức z = 6 + 7 i . Số phức liên hợp của z có điểm biểu diễn hình học là:
A. (-6;-7)
B. (6;7)
C. (6;-7)
D. (-6';7)
Cho số phức z thỏa mãn
z
1
2
và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức
w
1
z
là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là A. Điểm M B. Điểm Q C. Điểm N D. Điểm P
Đọc tiếp
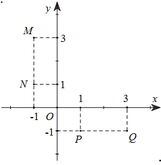
Cho số phức z thỏa mãn z = 1 2 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w = 1 z là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là
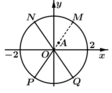
A. Điểm M
B. Điểm Q
C. Điểm N
D. Điểm P
suy ra điểm biểu diễn số phức w là điểm Q. Chọn B.
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
2
2
và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức
w
1
i
z
là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là A. Điểm Q B. Điểm M C. Điểm N D. Điểm P
Đọc tiếp
Cho số phức z thỏa mãn z = 2 2 và điểm A trong hình vẽ bên là điểm biểu diễn của z. Biết rằng trong hình vẽ bên, điểm biểu diễn của số phức w = 1 i z là một trong bốn điểm M, N, P, Q. Khi đó điểm biểu diễn của số phức w là
A. Điểm Q
B. Điểm M
C. Điểm N
D. Điểm P
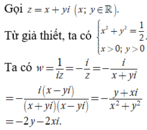
Vì x > 0, y > 0 nên điểm biểu diễn số phức w có tọa độ là (-2y;-2x) (đều có hoành độ và tung độ âm). Đồng thời 
Suy ra điểm biểu diễn của số phức w nằm trong góc phần tư thứ III và cách gốc tọa độ O một khoảng bằng 2OA. Quan sát hình vẽ ta thấy có điểm P thỏa mãn. Chọn D.
Đúng 0
Bình luận (0)