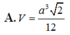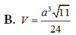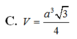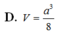Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng:
Đọc tiếp
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng:
Những câu hỏi liên quan
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng A.
a
3
2
6
B.
a
3
2
12
C.
a
3
2
3...
Đọc tiếp
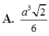
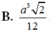
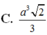
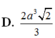
Cho khối tứ diện đều có tất cả các cạnh bằng 2a. Thể tích khối tứ diện đã cho bằng
A. a 3 2 6
B. a 3 2 12
C. a 3 2 3
D. 2 a 3 2 3
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng A.
4
2
a
3
3
B.
8
a
3
3
C.
8
2...
Đọc tiếp
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng
A. 4 2 a 3 3
B. 8 a 3 3
C. 8 2 a 3 3
D. 2 2 a 3 3
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng A.
2
a
3
4
B.
8
a
3
3
C.
8...
Đọc tiếp
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng
A. 2 a 3 4
B. 8 a 3 3
C. 8 2 a 3 3
D. 2 2 3 3
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a . Thể tích của khối chóp đã cho bằng A.
4
2
a
3
3
B.
8
a
3
3
C.
8
2
a
3...
Đọc tiếp
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a . Thể tích của khối chóp đã cho bằng
A. 4 2 a 3 3
B. 8 a 3 3
C. 8 2 a 3 3
D. 2 2 a 3 3
Đáp án A
Phương pháp:
Sử dụng công thức giải nhanh tính thể tích khối chóp tứ giác đều có cạnh bằng a là: V = a 3 2 6
Cách giải:
Với bài toán, khối chóp tứ giác có cạnh bằng 2a nên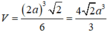 
Đúng 0
Bình luận (0)
Cho khối chóp tứ giác đều có tất cả các cạnh bằng 2a. Thể tích của khối chóp đã cho bằng
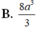
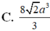
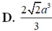
Chọn A
Thể tích khối chóp tứ giác đều cạnh a là
Đúng 0
Bình luận (0)
Cho khối tứ diện ABCD có
A
B
x
, tất cả các cạnh còn lại bằng 2. Thể tích khối tứ diện đã cho đạt giá trị lớn nhất bằng A.
1
2
B.
3
3
2
C.
2
2
3
D. 1
Đọc tiếp
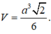
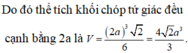
Cho khối tứ diện ABCD có A B = x , tất cả các cạnh còn lại bằng 2. Thể tích khối tứ diện đã cho đạt giá trị lớn nhất bằng
A. 1 2
B. 3 3 2
C. 2 2 3
D. 1
Chọn đáp án D
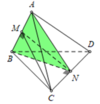
Gọi M,N lần lượt là trung điểm AB, CD
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng A.
3
a
3
24
.
B.
2
π
a
3
24
....
Đọc tiếp
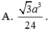
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
A. 3 a 3 24 .
B. 2 π a 3 24 .
C. 2 2 a 3 9 .
D. 3 π a 3 8 .
Đáp án B
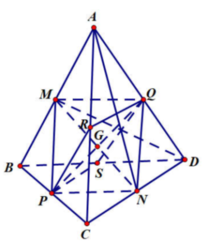
Gọi G là trọng tâm tứ diện ABCD. Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện.
Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, BC, AD, AC, BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS.
Δ A C D = Δ B C D ⇒ A N = B N ⇒ Δ N A B cân tại N ⇒ M N ⊥ A B
Tương tụ ta có M N ⊥ C D .
Ta có: P Q = R S = M N = A N 2 − A M 2 = a 3 2 2 − a 2 4 = a 2 2 .
Suy ra d G , A B = d G , C D = 1 2 M N = a 2 4 .
Chứng minh tương tự ta có d G , A C = d G , A D = d G , B D = d G , B C = a 2 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD.
Bán kính mặt cầu R = a 2 4 . Suy ra thể tích khối cầu là V = 4 3 π R 3 = 4 3 π a 2 4 3 = 2 π a 3 24 .
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
