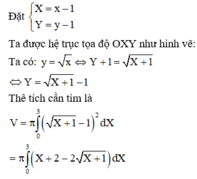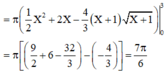Cho (H) là hình phẳng giới hạn bởi đồ thị hàm số y = - e x + 4 x , trục hoành và hai đường thẳng x=1;x=2; V là thể tích của khối tròn xoay thu được khi quay hình (H) quanh trục hoành. Khẳng định nào sau đây đúng?
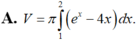
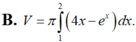
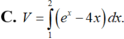
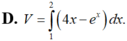
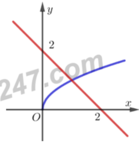
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
cho hình phẳng h được giới hạn bởi đồ thị hàm số y = e mũ 2x trục Ox Oy và đường thẳng x = 2 tính s hình phẳng trên
Tham khảo:
Do \(ex>0;∀xex>0;∀x\)
Diện tích hình phẳng:
\(S=2∫0exdx=ex|20=e2−1\)
Cho hình (H) là hình phẳng giới hạn bởi 2 đồ thị của 2 hàm số y = x 2 và y = x+2 Diện tích của hình (H) bằng
A. 7/6
B. -9/2
C. 3/2
D. 9/2
Cho hình (H) là hình phẳng giới hạn bởi 2 đồ thị của 2 hàm số y = x2 và y = x+2. Diện tích của hình (H) bằng
A. 7/6
B. - 9/2
C. 3/2
D. 9/2
Đáp án D
Phương pháp:
Diện tích hình phẳng tạo bởi hai đồ thị hàm số y = f(x), y = g(x) và các đường thẳng x = a, x = b, a<b

Cách giải: Phương trình hoành độ giao điểm của y = x2 và y = x+2
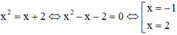
Diện tích hình (H):

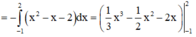
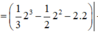
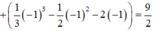
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là:
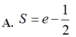
![]()
![]()
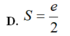
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x = 1 thì diện tích hình (H) là:
A. S = e - 1 2
B. S = 2 e - 1
C. S = 1
D. S = e 2
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x . e x , trục hoành, trục tung và đường thẳng x=1 thì diện tích hình (H) là
A. S = e − 1 2
B. S = 2 e − 1
C. S = 1
D. S = e 2
Cho hình phẳng (H) giới hạn bởi đồ thị hàm số y = x − 1 x + 2 và các đường thẳng Δ : y = 2 , d : − 2 x − 4 (tham khảo hình bên). Tính diện tích hình phẳng (H)
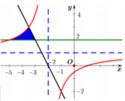
A. 1 4 + 3 ln 2
B. 1 4
C. − 2 + 3 ln 3
D. − 5 4 + 3 ln 2
Đáp án D
Hoành độ giao điểm của (H) và (d) là nghiệm: x − 1 x + 2 = − 2 x − 4 ⇔ x = − 1 x = − 7 2
Hoành độ giao điểm của (d) và Δ là nghiệm: 2 = − 2 x − 4 ⇔ x = − 3
Hoành độ giao điểm của (H) và Δ là nghiệm: x − 1 x + 2 = 2 ⇔ x = − 5
Khi đó, diện tích hình phẳng cần tính là S = ∫ − 5 − 7 2 x − 1 x + 2 − 2 d x + ∫ − 7 2 − 3 − 2 x − 4 − 2 d x = − 5 4 + 3 ln 2
Cho H là hình phẳng giới hạn bởi các đồ thị hàm số y = e , y = e x và y = 1 − e x + 1 (tham khảo hình vẽ). Diện tích của H là
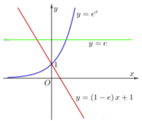
A. S = e + 1 2
B. S = e + 3 2
C. S = e − 1 2
D. S = e + 1 2
Đáp án A
Xét hệ giao điểm:
y = e y = 1 − e x + 1 ⇔ y = e x = − 1
Xét hệ giao điểm:
y = e x x = e ⇔ x = 1 y = e
Dựa vào hình vẽ ta có:
S = ∫ − 1 0 e − 1 − e x − 1 d x + ∫ 0 1 e − e x d x
= ∫ − 1 0 e − 1 x + 1 d x + e x − e x 0 1 = e − 1 x 2 2 + x − 1 0 + 1 = 1 2 e − 1 + 1 = 1 2 e + 1
Cho hình phẳng (H) giới hạn bởi đồ thị các hàm số sau y = x , y = 1 đường thẳng x = 4 (tham khảo hình vẽ). Thể tích khối tròn xoay sinh bởi hình (H) khi quay quanh đường thẳng y = 1 bằng

A. 9 2 π
B. 119 6 π
C. 7 6 π
D. 21 2 π
Chọn C.

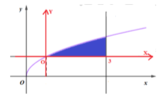

Ta được hệ trục tọa độ OXY như hình vẽ: