Chứng minh 1^3+2^3+3^3+...+n^3 là số chính phương

Những câu hỏi liên quan
Bài 1: Chứng minh một số tự nhiên gôm 27 chữ số 3 và 49 chứ số 7 đều chính phương
Bài 2: Chứng minh
A=12+22+32+...+562 không là số chính phương
B=1+3+5+7+...+n là số chính phương
Bài 3: Tìm hai số tự nhiên k và n sao cho k2=2006+n2
Chứng minh : \(1+2^3+3^3+4^3+.....+\left(n-1\right)^3+n^3\)( n thuộc N) là 1 số chính phương !
chứng minh : 1 mũ 3 + 2 mũ 3 + ... + n mũ 3 là số chính phương
an = n(n + 1) (n + 2) (n + 3) + 1
= (n2 + 3n) (n2 + 3n + 2) + 1
= (n2 + 3n)2 + 2(n2 + 3n) + 1
= (n2 + 3n + 1)2
Với n là số tự nhiên thì n2 + 3n + 1 cũng là số tự nhiên, theo định nghĩa, an là số chính phương.
Đúng 0
Bình luận (0)
chứng minh rằng : tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương: 1 mũ 3 + 2 mũ 3 +..... + n mũ3 =(1+2+.....+n) mũ 2
Giả sử 1^3+2^3+...+n^3=(1+2+...+n)^2(1)
Khi n=1 thì ta sẽ có 1^3=1^2(đúng)
Giả sử (1) đúng khi n=k
Khi n=2 thì ta sẽ có 1^3+2^3=9=(1+2)^2
Ta sẽ cần chứng minh (1) đúng khi n=k+1
1^3+2^3+...+n^3
=1^3+2^3+...+k^3+(k+1)^3
=(1+2+3+...+k)^2+(k+1)^3
Xét biểu thức (k+1)^2+2(k+1)(1+2+...+k)
=(k+1)^2+2*(k+1)*k*(k+1)/2
=(k+1)^2*(1+k)=(k+1)^3
=>1^3+2^3+...+(k+1)^3
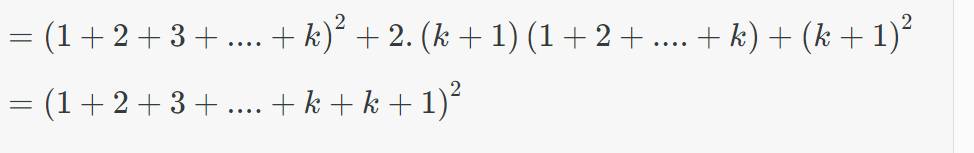
=>ĐPCM
Đúng 0
Bình luận (0)
chứng minh rằng tổng lập phương các số tự nhiên liên tiếp từ 1 là một số chính phương : 1+3+5+...+ n mũ 3 =(1+2+...+ n) mũ 2
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
1. Chứng minh tổng các số tự nhiên liên tiếp từ 1 đến 2005 không phải là số chính phương.
2. Chứng minh số : n = 20044 + 20043 + 20042 + 23 không là số chính phương.
3.Chứng minh số : n = 44 + 4444 + 444444 + 44444444 + 15 không là số chính phương.
4.Chứng minh số 4014025 không là số chính phương.
Chứng minh rằng 13+23+.......+n3 là một số chính phương
Hãy chứng minh 1+2+3+4+5+6+...+(n-1)+n+(n-1)+...+3+2+1 là số chính phương ?
Biết n thuộc N
Chứng minh 1^3+2^3+3^3+...+2016^3 là số chính phương
Tham khảo đề bài và cách làm nha bạn !
Đề bài : chứng minh số 1^3+2^3+3^3+...+10^3 là số chính phương .
Giải
Ta có : 13 + 23 + 33 + ... + 103= 102 . (10 + 1 ) 2 \(⋮\) 4 = 4. 52 .112\(⋮\)4 = 52 . 112 = (5.11 )2= 552 là số chính phương
\(1^3+2^3+3^3+...+2016^3\)
\(=2016^2.\left(2016+1\right)^2\)
\(=2016^2.2017^2\)
\(=\left(2016.2017\right)^2\) là số chính phuong
ti.k nhanh nha bn
















