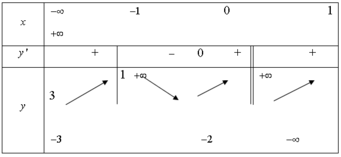
Cho hàm số y = f(x) xác định trên  ℝ  và có đạo hàm f '(x)  thỏa mãn  f ' x = 1 - x x + 2 . g x + 2018  trong đó g x < 0 , ∀ x ∈ ℝ . Hàm số y = f 1 - x + 2018 x + 2019  nghịch biến trên khoảng nào?

A.  1 ; + ∞

B.  0 ; 3

C.  - ∞ ; 3

D.  3 ; + ∞

Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ  và có đồ thị f'(x) như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây? 

Cho hàm số y= f(x) xác định trên  ℝ  và có bảng xét dấu của đạo hàm như sau:

Khi đó số điểm cực trị của hàm số y= f(x) là:

A. 3

B. 2

C. 4

D. 1

Cho hàm số y= f(x) xác định và có đạo hàm trên  ℝ  thỏa mãn  f 1 + 2 x 2 = x - f 1 - x 3 .  Viết phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm có hoành độ bằng 1.

A.  y = - 1 7 x - 6 7

B.  y = 1 7 x - 8 7

C.  y = - 1 7 x + 8 7

D.  y = - x + 6 7

Cho hàm số y = f(x) xác định trên R và có đạo hàm y = f '(x) thỏa mãn f ' x = 1 − x x + 2 . g x + 2018  trong đó g x < 0 ,   ∀ x ∈ ℝ .  Hàm số y = f 1 − x + 2018 x + 2019  nghịch biến trên khoảng nào?

A.  1 ; + ∞ .

B. (0;3)

C.  − ∞ ; 3 .

D.  3 ; + ∞ .

Hàm số y = f ( x ) xác định và liên tục trên R có đạo hàm f ' ( x ) = x - 1 3 x - 2 2 x 3 , ∀ x ∈ ℝ . Số điểm cực trị của hàm số y = f ( x ) là

A. 3

B. 1

C. 0

D. 2

Cho hàm số  xác định trên ℝ  và có bảng xét dấu của đạo hàm như sau:

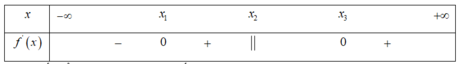
Khi đó số điểm cực trị của hàm số y = f (x) là:

A. 3.

B. 2.

C. 4.

D. 1.

Cho hàm số f x có đạo hàm f ' x  xác định, liên tục trên ℝ và có đồ thị  f ' x  như hình vẽ bên. Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?

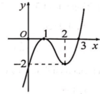
A.  2 ; + ∞

B.  - ∞ ; 1

C.  3 ; + ∞

D.  1 ; 3

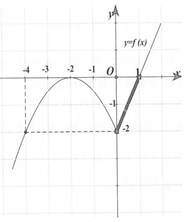
Cho hàm số y=f(x) có đạo hàm xác định trên tập ℝ / 0  và đồ thị hàm số y=f(x)  như hình vẽ bên dưới. Có bao nhiêu giá trị nguyên của tham số m để phương trình f cos 2 x = m  có nghiệm?

A. Không tồn tại m

B. 1

C. 2

D. 3

Cho hàm số f(x) có đạo hàm f'(x) xác định, liên tục trên ℝ và có đồ thị f'(x) như hình vẽ bên. Khẳng định nào sau đây là đúng?

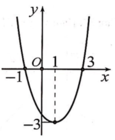
A. Hàm số y=f(x) đồng biến trên khoảng 1 ; + ∞ .

B. Hàm số y=f(x)đồng biến trên khoảng - ∞ ; - 1  và  3 ; + ∞ .

C. Hàm số y=f(x) nghịch biến trên khoảng  - ∞ ; - 1 .

D. Hàm số y=f(x) đồng biến trên khoảng (1;3).