Cho mặt cầu (S) : x 2 + y 2 + z 2 -2x + 4y + 2z - 3 = 0 . Tính bán kính R của mặt cầu (S).
A. R= 3
B. R = 3 3
C. R = 3
D. R= 9
#2H3Y1-3~Trong không gian với hệ tọa độ Oxyz. Tìm tâm I và tính bán kính R của mặt cầu (S): x²+y²+z²-2x-4y+2z+2=0.
A. I(-1;-2;1),R=2
B. I(1;2;-1),R=2√2
C. I(-1;-2;1),R=2√2
D. I(1;2;-1),R=2.
Đáp án D
Mặt cầu (S) có tâm I(1;2;-1) và bán kính ![]()
Cho mặt cầu (S): x 2 + y 2 + z 2 - 2x + 4y - 2z - 3 = 0 cắt 2 mặt phẳng (P): x - 2y + z = 0 và (Q): x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 ; r 2 . Khi đó tỉ số r 1 r 2 bằng
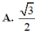
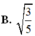
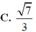
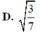
Chọn D
Mặt cầu (S) có tâm I(1;-2;1), bán kính R = 3
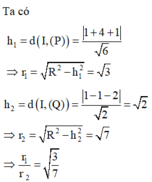
Trong không gian tọa độ Oxyz, cho mặt cầu (S): ( x - 2 ) 2 + y 2 + ( z + 1 ) 2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C)
![]()
![]()
![]()
![]()
Trong không gian tọa độ Oxyz, cho mặt cầu (S): (x-2)2 + y2 + (z+1)2 = 9 và mặt phẳng (P): 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính R của (C).
![]()
![]()
![]()
![]()
Cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Tính bán kính R của mặt cầu (S).
A. R = 3
B. R = 3 3
C. R = 3
D. R = 9
Cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y - 2 z - 3 = 0 cắt 2 mặt phẳng P : x - 2 y + z = 0 và Q : x - z - 2 = 0 theo các đường tròn giao tuyến với bán kính r 1 , r 2 . Khi đó tỉ số r 1 r 2 bằng
A. 3 2
B. 3 5
C. 7 3
D. 3 7
Đáp án D
Mặt cầu (S) có tâm I(1;-2;1), bán kính R = 3
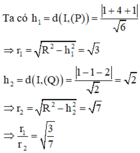
Trong không gian Oxyz, cho mặt cầu S : x 2 + y 2 + z 2 - 2 x + 4 y + 2 z - 3 = 0 . Tính bán kính R của mặt cầu (S).
A. R = 3
B. R = 9
C. R = 3 3
D. R = 3
Đáp án A
Xét mặt cầu: S : x - 1 2 + y + 2 2 + z + 1 2 = 9 ⇒ bán kính R = 3.
Trong không gian Oxyz, cho mặt phẳng (P): 2x + y + 2z + 2 =0 và cho mặt cầu ( S ) : ( x - 2 ) 2 + ( y - 1 ) 2 + ( z - 1 ) 2 = 10 Bán kính của đường tròn giao tuyến giữa (P) và (S) là
A. 7
B. 10
C. 3
D. 1
trong không gian tọa độ oxyz , cho mặt cầu (s) : (x-2)^2+y^2+(z+1)^2=9 và mặt phẳng (P) : 2x-y-2z-3=0. Biết rằng mặt cầu (S) cắt (P) theo giao tuyến là đtròn (C) . Tính bán kính R của (C)
giúp mình vs ạ . mình cảm ơn