Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2 và x . f ' x = xf 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng

A. .

B. .

C. .

D. .

Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2  và x . f ' x = x f 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng

A.  3 2 e

B.  4 3 e

C.  3 4 e

D.  2 3 e

Cho hàm số y=f(x) liên tục, có đạo hàm trên [-1;0]. Biết f’(x) = (3x²+2x)e^-f(x)  ∀ x ∈ - 1 ; 0 Tính giá trị biểu thức A=f(0)-f(-1) 

Cho hàm số y=f(x) có đạo hàm liên tục trên R. Biết f(1)=e và ( x + 2 ) f ( x ) = x f ' ( x ) - x 3 , với mọi x thuộc R. Tính f(2).

A.  4 e 2 - 4 e + 4

B.  4 e 2 - 2 e + 1

C. 2 e 3 - 2 e + 2

D.  4 e 2 + 4 e - 4

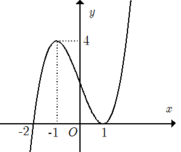
Cho hàm số  y= f( x) = ax4+ bx3+ cx2+ dx+ e với a ≠0. Biết rằng hàm số y= f( x) có đạo hàm là f’(x)  và hàm số y= f’(x) có đồ thị như hình vẽ bên. Khi đó nhận xét nào sau đây là sai?

A. Trên khoảng (-2; 1)  thì hàm số y= f( x) luôn tăng.

B. Hàm số y= f(x)   giảm trên đoạn [ -1; 1] .

C. Hàm số y= f( x)  đồng biến trên khoảng  (1+ ∞) .

D. Hàm số y= f( x)  nghịch biến trên khoảng (- ∞; -2)

Cho hàm số  f ( x ) = a x 4 + b x 3 + c x 3 + d x + e ( a ≠ 0 ) . Biết rằng hàm số f(x) có đạo hàm là f’(x) và hàm số y=f’(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?

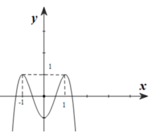
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)

B. Hàm số f(x) đồng biến trên khoảng (0;+∞)

C. Hàm số f(x) đồng biến trên khoảng (-2;1)

D. Hàm số f(x) nghịch biến trên khoảng (-∞;-2)

Cho hàm số y= f(x) có đạo hàm liên tục trên khoảng thỏa mãn x 2 f ' x + f x = 0 và f x ≠ 0 , ∀ x ∈ 0 ; + ∞ . Tính f(2) biết f(1) = e.

A. .

B. .

C. .

D. .

Cho hàm số f(x) có đạo hàm trên R thỏa mãn f ' x - f x = x 2 + 1 e x 2 + 2 x - 1 2 , và f(1) = e. Giá trị của f(5) bằng

A. .

B. .

C. .

D. .

Cho hàm số f x = a x 4 + b x 3 + c x 3 + d x + e   a ≠ 0  . Biết rằng hàm số f(x) có đạo hàm là f'(x) và hàm số y=f'(x) có đồ thị như hình vẽ dưới. Khi đó mệnh đề nào sau đây sai?

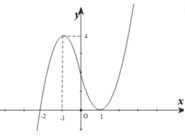
A. Hàm số f(x) nghịch biến trên khoảng (-1;1)

B. Hàm số f(x) đồng biến trên khoảng 0 ; + ∞  

C. Hàm số f(x) đồng biến trên khoảng (-2;1)

D. Hàm số f(x) nghịch biến trên khoảng  - ∞ ; - 2