CMR: 1028 + 8 chia hết cho 72

Những câu hỏi liên quan
cmr 1028+8 : 72 day la cm chia hết nha em ko biet viet dau chia hết
1028 + 8 = 1036
1036 chia 72 được thương 14 dư 28 mà
Đúng 0
Bình luận (0)
Chứng minh rằng F= 10 28 + 8 chia hết cho 72
CHỨNG TỎ
1028+8 CHIA HẾT CHO 72
Bạn nhầm rồi 1028+8 = 1036 không chia hết cho 9 nhé nên không chia hết cho 72
Đúng 0
Bình luận (0)
Chứng minh rằng:
a) 10n chia 9 dư 1 ( n e N )
b) 1028 + 8 chia hết cho 72
CMR 1028 + 8 : 72
có 2 cách nhé
cách 1: vì 1028+8=1036, mà 1036 chia hết cho 7
cách 2 :1028 : 7(dư 6)
8 : 7(dư1)
ta có 6+1=7 , 7 chia hết cho 7
vậy 1028 + 7 chia hết 72
ủng hộ nhé
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1 Tìm các chữ số a,b biết
a. 7a5b1 chia hết cho 3 và a- b = 4
b. {4a7 + 1b5} chia hết cho 9 và a- b = 6
c. 62ab4a7 chia hết cho 99
2 Chứng minh rằng H = 1028 + 8 chia hết cho 72
giúp mình với mình tickk cho
bt àm câu a thôi '
7a5b1 \(⋮3\Leftrightarrow\left(7+a+5+b+1\right)⋮3\Leftrightarrow\left(13+a+b\right)⋮3\)
\(\Rightarrow a+b\in\left\{2,5,8,11,14,17\right\}\)
Vì a-b=4 là chẵn\(\Rightarrow a+b\)và
a+b > 4 nên \(a+b\in\left\{8,14\right\}\)
+Nếu a+b=8 a-b=4
thì a=6
b=2
+Nếu a+b=14 a-b=4
thì a=9
b=5
Vậy a=6 và b=2
a=9 và b=5
Đúng 1
Bình luận (0)
Chứng tỏ 1028+8 chia hết cho 9
ta có :1028+8=+8=100...00(28 chữ số 0)+8⋮9(vì 1 + 8=9⋮9)
vậy 1028+8⋮9 thỏa mãn
Đúng 1
Bình luận (1)
chứng tỏ 1028+8 chia hết cho 18
A = 1028 + 8
A = \(\overline{100...08}\) ( 27 chữ số 0)
Xét tổng các chữ số của A ta có: 1 + 0 x 27 + 8 = 9 ⋮ 9 ⇒A ⋮ 9
A = \(\overline{...8}\) ⋮ 2 ⇒ A \(\in\)BC(2; 9); 2 = 2; 9 = 32; BCNN(2; 9) = 2.32 = 18
⇒ A \(\in\) B(18) hay A ⋮ 18 (đpcm)
Đúng 0
Bình luận (0)
1028+8/chứng tỏ chia hết cho 9
giúp mình với
TL:
Ta có: \(10^{28}+8=100...00\)(\(28\) chữ số \(0\)) \(+8⋮9\) ( Vì \(1+8=9⋮9\))
Vậy\(10^{28}+8⋮9\) thoả mãn bài toán
CHÚC BẠN HỌC TỐT NHÉ.
Đúng 1
Bình luận (2)
1028 + 8 chia hết cho 9
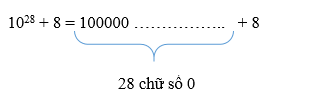
1028 + 8 = 1 + 0 + 0 + ............... + 8 = 9
Mà \(9⋮9\)
\(\Rightarrow10^{28}+8⋮9\)
Đúng 1
Bình luận (0)
Chứng minh rằng F = 10 28 + 8 chia hết cho 9



























