Hình bình hành ABCD có đường cao AH và AK bằng nhau.Chứng minh rằng tứ giác ABCD là hình thoi

Những câu hỏi liên quan
a) Cho hình thoi ABCD. Kẻ hai đường cao AH, AK. Chứng minh rằng AH = AK ?
b) Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi ?
Giải:
a) Hình vẽ:
Xét hai tam giác vuông \(AHD\) và \(AKB\) ta có:
\(AD=AB\) (cạnh hình thoi)
\(\widehat{D}=\widehat{B}\) (hai góc đối hình thoi)
Do đó: \(\Delta AHD=\Delta AKB\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\) (Đpcm)
b) Hình vẽ:
Cách 1: Ta có: \(\Delta AHD=\Delta AKB\left(g.c.g\right)\)
\(\Rightarrow AD=AK\)
Hình bình hành \(ABCD\) có hai cạnh kề bằng nhau nên là hình thoi (Đpcm)
Cách 2: Ta có: \(\Delta AHC=\Delta AKC\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{C_1}=\widehat{C_2}\)
Hình bình hành \(ABCD\) có một đường chéo là phân giác của một góc nên là hình thoi (Đpcm)
Đúng 0
Bình luận (1)
a) cho hình thoi ABCD . kẻ hai đường cao AH , AK . Chứng minh rằng AH=AK
b) hình bình hành ABCD có hai đường cao AH,AK bằng nhau . Chứng minh rằng ABCD là hình thoi
a,xét 2 tan giác vuông ABH và AKD có:
^H=^K=90ĐỘ
ab=ad(GT)
^B=^D(T/C hình thoi)
=>tam giác AHB=tam giác AKD( cạnh huyền-góc nhọn)
=>AH=AK
b,ta có:^a1+^a2=90độ (tổng 2 góc nhọn trong tam giác vuông)
^a2+^b=90độ(như trên)
mà ^d=^b( 2 góc đối)
=>^a1=^a2
xét tam giác ADH và ABK có:
^a1=^a2(cmt)
AH=AK(gt)
^h=^k=90độ
=>tam giác ADH=ABK(g.c.g)=>AD=AB(tương ứng)
-hình bình hành có 2 cạnh liên tiếp AD=AB
=>ABCD là hình thoi
=>
Đúng 0
Bình luận (0)
xét \(\Delta\)ACK và ABH có
AB=AC(tc hình thoi)
\(\widehat{AKC}=\widehat{AHB}=90^o\)
\(\widehat{B}=\widehat{C}\)
theo trường hợp cạnh huyền góc nhọn
=>AH=AK (2 cạnh tương ứng)
b)
xét \(\Delta\)AKDvà \(\Delta\)AHB
có\(\widehat{AHB}=\widehat{AK\text{D}}=90^o\)
AH=AK(gt)
\(\widehat{B}=\widehat{D}\)(tính chất HBH)
=>AB=AD(2 cạnh tương ứng)
ABCD là hình thoi vì là HBH có 2 cạnh kề bằng nhau
Đúng 0
Bình luận (0)
Hình bình hành ABCD có hai đường cao AH, AK bằng nhau. Chứng minh rằng ABCD là hình thoi
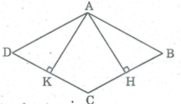
Xét hai tam giác vuông AHC và AKC, ta có:
∠ (AHC) = ∠ (AKC) = 90 0
AH = AK (gt)
AC cạnh huyền chung
Suy ra: ∆ AHC = ∆ AKC (cạnh huyền- cạnh góc vuông)
⇒ ∠ (ACH) = ∠ (ACK) hay ∠ (ACB) = ∠ (ACD)
⇒ CA là tia phân giác ∠ (BCD)
Hình bình hành ABCD có đường chéo CA là đường phân giác nên là hình thoi.
Đúng 0
Bình luận (0)
Bài 1) Cho tam giác ABC, vẽ hai trung tuyến BM và CN. Trên tia đối của tia MB và NC lần lượt lấy 2 điểm D và E sao cho MDMB và NCNEa) Chứng minh: ABCD là hình bình hành b) Chứng minh: A là trung điểm của ED c) Tam giác ABC phải thõa mãn điều kiện gì để BCDE là hình thang cân Bài 2) Cho hình thoi ABCD, gọi O là giao điểm của 2 đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, 2 đường thẳng đó cắt nhau ở K a) Tứ giác OKBC là hình gì? Vì sao?b) CMR: AB...
Đọc tiếp
Bài 1) Cho tam giác ABC, vẽ hai trung tuyến BM và CN. Trên tia đối của tia MB và NC lần lượt lấy 2 điểm D và E sao cho MD=MB và NC=NE
a) Chứng minh: ABCD là hình bình hành
b) Chứng minh: A là trung điểm của ED
c) Tam giác ABC phải thõa mãn điều kiện gì để BCDE là hình thang cân
Bài 2) Cho hình thoi ABCD, gọi O là giao điểm của 2 đường chéo. Vẽ đường thẳng qua B và song song với AC, vẽ đường thẳng qua C và song song với BD, 2 đường thẳng đó cắt nhau ở K
a) Tứ giác OKBC là hình gì? Vì sao?
b) CMR: AB=OK
c) Tìm điều kiện của hình thoi ABCD để tứ giác OBKC là hình vuông
Bài 3) Cho tứ giác ABCD. Gọi E,F,G,H theo thứ tự là trung điểm của AB,BC,CD,DA
a) Chứng minh E F G H là hình bình hành
b) Các đường chéo AC,BD của tứ giác ABCD có điều kiện gì thì EFGH là hình chữ nhật, hình thoi,hình vuông?
Bài 4) a) Cho hình thoi ABCD. Kẻ 2 đường cao AH,AK. Chứng minh rằng: AH=AK
b) Hình bình hành ABCD có 2 đường cao AH=AK Chứng minh rằng ABCD là hình thoi
Mọi người giúp với ạ mình đang ôn tập đề cương .........
Bài này có gì đâu em ! Anh làm nhé !
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Đúng 0
Bình luận (0)
Chuyển vế cái cần chứng minh ta được
1/AB^2 - 1/AE^2 =1/4AF^2
hay ( AE^2 - AB^2)/AB^2.AE^2 = 1/4AF^2
hay BE^2/ 4BC^2.AE^2 = 1/AF^2
Nhân chéo hai vế ta có : BC.AE = BE.AF hay là BC/AF = BE/AE
Đúng 0
Bình luận (0)
cho hình bình hành ABCD kẻ AH vuông góc với DC tại H, AK vuông góc với BC tại K. chứng minh nếu AH=AK thì tứ giác ABCD là hình thoi
Xét ΔAHD vuông tại H và ΔAKB vuông tại K có
AH=AK
góc HAD=góc KAB
=>ΔAHD=ΔAKB
=>AD=AB
=>ABCD là hình thoi
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD . Tứ giác A,H hạ AH ,AK lâng lượt vuông góc với BD .chứng minh rằng tues giác AHCK cũng là hình bình hành
Sửa đề: Từ A,C hạ AH,CK lần lượt vuông góc với BD
Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
=>AH=CK
AH\(\perp\)BD
CK\(\perp\)BD
Do đó: AH//CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi E , F thứ tự là trung điểm của AB và CD.
Đường thẳng BD cắt AF và CE thứ tự tại G và H. Chứng minh rằng:
a) Tứ giác EGFH là hình bình hành.
b) Hình hình hành ABCD phải có thêm điều kiện gì thì tứ giác EGFH là hình chữ
nhật, hình thoi.
Cho hình bình hành ABCD. Gọi E , F thứ tự là trung điểm của AB và CD.
Đường thẳng BD cắt AF và CE thứ tự tại G và H. Chứng minh rằng:
a) Tứ giác EGFH là hình bình hành.
b) Hình hình hành ABCD phải có thêm điều kiện gì thì tứ giác EGFH là hình chữ
nhật, hình thoi.
Cho hình thang ABCD gọi M, N, P, Q lần lượt là trung điểm của hai đáy và hai đường chéo của hình thang.
a) Chứng minh rằng tứ giác MPNQ là hình bình hành.
b) Hình thang ABCD phải có thêm điều kiện gì để tứ giác MPNQ là hình thoi?
a) Áp dụng tính chất đường trung bình của tam giác cho DABC và DDBC ta sẽ có:
MQ//PN//BC và MQ = PN = 0.5BC ÞMPNQ là hình bình hành.
b) Tương tự ta có QN//MP//AD và QN = MP = 0.5AD.
Nên để MPNQ là hình thoi thì MN ^ PQ khi đó MN ^ CD và trung trực hay trục đối xứng của AB và CD.
Þ hình thang ABCD là hình thang cân
Đúng 0
Bình luận (0)























