Cho hàm số y = x 3 - x 2 + m x - 2 có đồ thị (C). Tìm m để đồ thị (C) có hai điểm cực trị A, B và đường thẳng AB vuông góc với đường thẳng d : y = 1 2 x + 1
A. m = 8 3
B. m = 1
C. m = - 8 3
D. m = - 26 3
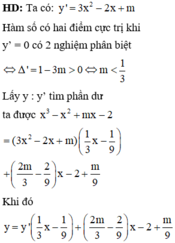
Phương trình đường thẳng đi qua 2 điểm cực trị là
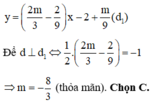
Cho hàm số y = x 3 - 12 x + 12 có đồ thị (C) và điểm A(m;-4). Gọi S là tập hợp tất cả các giá trị thực của m nguyên thuộc khoảng (2;5) để từ A kẻ được ba tiếp tuyến với đồ thị (C). Tổng tất cả các phần tử nguyên của S bằng
A. 7
B. 9
C. 3
D. 4
Chọn A
Gọi phương trình tiếp tuyến đi qua A là
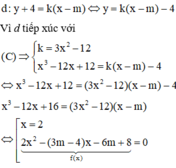
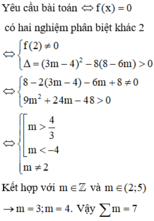
Đồ thị hàm số y = 2 x 3 +m x 2 -12x-13 có hai điểm cực trị cách đều trục tung khi và chỉ khi:
A.m=-1
B.m=0
C.m=-1;m=-2
D.m=-2
Cho hàm số y = x 3 + 2 ( m + 1 ) x 2 + 3 mx + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d:y=-x +2 cắt đồ thị (C ) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6 .
A.m= -2.
B. m= -2 hoặc m= 3.
C. m= 3.
D. Không tồn tại m.
Với giá trị nào của m, đồ thị hàm số y = x 3 + 3 x 2 + m 2 x + m có hai điểm cực trị đối xứng qua đường thẳng: y = 1 2 x - 5 2
A. m = 0
B. m = 1
C. m = -1
D. Không tồn tại
Chọn D
y ' = 3 x 2 + 6 x + m 2 . Hàm số có hai điểm cực trị => y’=0 có hai nghiệm phân biệt <=> Δ ' = 3 2 - 3 . m 2 > 0 <=> - 3 < m < 3
Chia y cho y’ ta được:
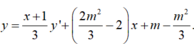
Giả sử x 1 , x 2 là hai nghiệm phân biệt của y’=0.
Phương trình đường thẳng đi qua hai điểm cực trị có dạng
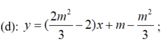
(d) có vectơ pháp tuyến là
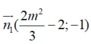
Vì hai điểm cực trị đối xứng với nhau qua (Δ) nên (d) ⊥ (Δ)
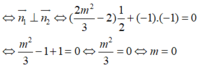
Thử lại khi m=0 ta có: y = x 3 + 3 x 2 ; y ' = 3 x 2 + 6 x ; y ' ' = 6 x + 6
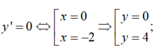
y''(0) = 6 > 0; y''(-2) = -6 < 0
Tọa độ hai điểm cực trị của đồ thị hàm số là O(0;0), A(-2;4)
Trung điểm của OA là I(-1;2).
Ta thấy I(-1,2) không thuộc đường thẳng (Δ) . Vậy không tồn tại m.
Cho hàm số y = x 3 + 2 m + 1 x 2 + 3 m x + 2 có đồ thị (C) và điểm M(3;1). Tìm tham số m để đường thẳng d: y = -x+2 cắt đồ thị (C) tại ba điểm phân biệt A(0;2),B,C sao cho tam giác MBC có diện tích bằng 2 6
A. m = -2
B. m = -2 hoặc m = 3
C. m = 3
D. Không tồn tại m
Cho hàm số y = 2 x + 1 2 x - m có đồ thị (C) và hai điểm A ( -2;3 ); C ( 4;1 ) . Tìm m để đường thẳng d : 3 x - y - 1 = 0 cắt đồ thị (C) tại hai điểm phân biệt B, D sao cho tứ giác ABCD là hình thoi
A. 8 3
B. 3 8
C. 4 3
D. 3 4
Đường thẳng AC qua A ( -2;3 ); C ( 4;1 ) nhận A C → = 6 ; - 2 làm vec tơ chỉ phương nên có phương trình là: x + 2 6 = y - 3 - 2 ⇔ y = - 1 3 x + 7 3
Tọa độ giao điểm của AC và BD là nghiệm của hệ phương trình 3 x - y - 1 = 0 y = - 1 3 x + 7 3 ⇔ x = 1 y = 2
Để ý rằng A C ⊥ B D và I là trung điểm AC.
Khi đó ABCD là hình thoi thì I ( 1;2 ) là trung điểm của BD.
Phương trình hoành độ giao điểm của (C) và d là: 2 x + 1 2 x - m = 3 x - 1 ⇔ 6 x 2 - 3 m + 4 x + m - 1 = 0
Do ∆ = 3 m + 4 2 - 4 . 6 m - 1 = 9 m 2 + 24 > 0 , ∀ m nên d luôn cắt (C) tại hai điểm phân biệt B và D.
Gọi x 1 , x 2 là hai nghiệm của phương trình (*). Theo định lý Viet ta có x 1 + x 2 2 = 3 m + 4 12
Đáp án A
Để I là trung điểm của BD thì 3 m + 4 12 = 1 ⇔ m = 8 3
Đáp án A
Cho hàm số y = x 3 + 6 x 2 + 12 x + 8 có đồ thị (C). Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên R.
B. Đồ thị (C) tiếp xúc với trục hoành.
C. Phương trình 
có một nghiệm với mọi m.
D. Hàm số đạt cực trị tại 
Cho hàm số y = x 3 + 6 x 2 + 12 x + 8 có đồ thị (C). Khẳng định nào sau đây là sai?
A. Hàm số đồng biến trên R
B. Đồ thị (C) tiếp xúc với trục hoành
C. Phương trình x 3 + 6 x 2 + 12 x + 8 = m có một nghiệm với mọi m
D. Hàm số đạt cực trị tại x= -2
