Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
![]()
![]()
![]()
![]()
Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình log ( ( m - 1 ) . 16 x + 2 . 25 x 5 . 20 x ) - 5 x + 1 . 4 x = ( 1 - m ) 4 2 x - 2 . 25 x có hai nghiệm thực phân biệt. Số phần tử của S bằng
A. 4.
B. 3.
C. 1.
D. 2.
Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
![]()
![]()
![]()
![]()
Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
![]()
![]()
![]()
![]()
Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
A. (0;+∞)
B. [0;+∞)
C. (-∞;0)
D. R
Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
A. ℝ
B. 0 ; + ∞
C. 0 ; + ∞
D. − ∞ ; 0

Chú ý: Phân biệt tập giá trị và tập xác định của hàm số logarit.
Tập hợp các số thực m để phương trình log 2 x = m có nghiệm thực là
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Tập hợp các số thực m để phương trình ln x 2 - m x - 2019 = ln x có nghiệm duy nhất là
A. ∅
B. - 1
C. 0
D. ℝ
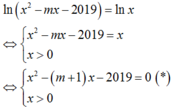
Nhận thấy phương trình (*) có a c < 0 ⇒ * có 2 nghiệm phân biệt, do đó ∀ m ∈ ℝ phương trình (*) luôn có 1 nghiệm thỏa mãn x > 0 .
Chọn D.
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.