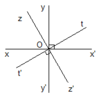
Cho bốn đường thẳng xx'. yy', zz', tt' cắt nhau tại O trong đó x O y ^ = 90 ° , z O t ^ = 90 ° . Trong đó có bao nhiêu góc bẹt, bao nhiêu góc vuông, bao nhiêu góc nhọn, bao nhiêu góc tù?
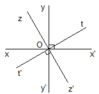
Cho bốn đường thẳng xx'. yy', zz', tt' cắt nhau tại O trong đó x O y ^ = 90 ° , z O t ^ = 90 ° . Trên hình vẽ có bao nhiêu góc?
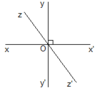
Vẽ ba đường thẳng xx’, yy’, zz’ cắt nhau tại O trong đó x O y ^ = 90 ° tia Oz nằm trong góc xOy. Trên hình vẽ có bao nhiêu góc?
Có 6 tia chung gốc nên có 6.5 2 = 15 (góc).
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
câu này bó tay chấm com chấm vn vì mình mới có lớp 5
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
+ Tổng số điểm phân biệt là: 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm
vẽ được 1 đường thẳng nên ta có 23. 22 : 2 = 253 đường thẳng.
0,25
+ Mặt khác số các điểm thẳng hàng là 5;6;7;8 nên số các đường thẳng
trùng nhau là 10,15,21,28. Số đường thẳng cần tìm là: 253 - 10 - 15 -
0,25
21 - 28 + 4 = 183 đường thẳng
Trên 4 đường thẳng xx' ; yy' ; zz' và tt' có số điểm phân biệt tương ứng là 5, 6, 7, 8 => Số tia lần lượt tương ứng là 10, 12, 14, 16 => Tổng số tia cần tìm là 10 + 12 + 14 + 16 = 52 tia.
Tổng số điểm phân biệt là : 4 + 5 + 6 + 7 + 1 = 23 điểm. Qua 2 điểm ta vẽ được 1 đường thẳng nên ta có 23 . 22 : 2 = 253 đường thẳng.
Mặt khác số các điểm thẳng hàng là 5, 6, 7, 8 nên số các đường thẳng trùng nhau là 10, 15, 21, 28. Số đường thẳng cần tìm là : 253 - 10 - 15 - 21 - 28 + 4 = 183 đường thẳng.
Cho bốn đường thẳng phân biệt xx’; yy’; zz’ và tt’ cắt nhau tại O. Lấy 4 điểm, 5 điểm, 6 điểm, 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên. Sao cho trong 3 điểm bất kỳ, mỗi điểm thuộc một đường thẳng khác nhau đều không thẳng hàng. Trên hình vẽ có bao nhiêu tia? Qua hai điểm vẽ được một đường thẳng, hỏi có thể vẽ được tất cả bao nhiêu đường thẳng?
Cho bốn đương thẳng phân biệt xx', yy' , zz' và tt' cắt hau tại O . Lấy 4 điểm , 5 điểm , 6 điểm , 7 điểm phân biệt khác điểm O lần lượt thuộc bốn đường thẳng trên . Sao cho trong 3 điểm bất kì , mỗi điểm thuộc một đương thẳng khác nhau đều không thẳng hàng . Trên hình vẽ có bao nhiêu tia ? Qua hai điểm vẽ được một đường thẳng , hỏi có thể vẽ được bao nhiêu đường thẳng?
trên hình vẽ có 52 tia
có 74 đường thẳng
mình làm vậy đó
Vẽ ba đường thẳng xx’, yy’, zz’ cắt nhau tại O trong đó x O y ^ = 90 ° tia Oz nằm trong góc xOy. Trong đó có bao nhiêu góc bẹt, bao nhiêu góc vuông, bao nhiêu góc nhọn, bao nhiêu góc tù?
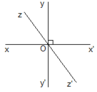
Trong đó có 3 góc bẹt x O x ' , y O y ' , z O z '
Có 4 góc vuông x O y , y O x ' , x ' O y ' , y ' O x
Có 4 góc nhọn x O z , z O y , x ' O z ' , z ' O y '
Có 4 góc tù x O z ' , x ' O z , y O z ' , z O y ' .
Vẽ ba đường thẳng xx ', yy ',zz ' cắt nhau tại O, trong đó xOy = 90o,tia Oz nằm trong góc xOy.
Vẽ 2 đường thẳng zz' và tt' cắt nhau tại O trong đó góc zot = 90 độ
a) Tính các góc còn lại
b) Vẽ đường thẳng xx' qua O sao cho tia ox nằm giữa ozvà ot . Có mấy ặp góc đối đỉnh nhọn, tù
\(a)\)
\(zz'\) và \(tt'\)cắt nhau tại \(O\)và có một góc vuông
=> Các góc còn lại đều vuông
\(\Rightarrow\widehat{tOz}=\widehat{zOt'}=\widehat{t'Oz'}=\widehat{tOz'}=90^o\)
\(b)\)
Có hai cặp góc nhọn đối đỉnh:
\(+)\)\(\widehat{xOt};\widehat{x'Ot'}\)
\(+)\)\(\widehat{xOz};\widehat{x'Oz'}\)
Có hai cặp góc tù đối đỉnh:
\(+)\)\(\widehat{xOt'};\widehat{x'Ot}\)
\(+)\)\(\widehat{x'Oz};\widehat{xOz'}\)