Có bao nhiêu mệnh đề dưới đây là đúng?
3 x > 2 x v ớ i ∀ x ∈ ℝ 4 x 2 ≥ 3 x 2 v ớ i ∀ x ∈ ℝ 81 x - 1 ≤ 3 x 2 v ớ i ∀ x ∈ ℝ 5 x + 3 x > 4 x v ớ i ∀ x ∈ ℝ 2 x + 3 x < 5 x v ớ i ∀ x > 1
A. 2
B. 3
C. 4
D. 5
Những câu hỏi liên quan
Cho các tập hợp:
M
{
x
∈
ℝ
:
x
≥
−
3
}
,
N
{
x
∈
ℝ
:
−
2
≤
x
≤
1
}
,
P
{
x
∈
ℝ
:
−
5
x
≤
0
}
.Mệnh đề nào sau đây là mệnh đề đúng? A.
M
⊂
N
B.
M
⊃
P
C. ...
Đọc tiếp
Cho các tập hợp:
M = { x ∈ ℝ : x ≥ − 3 } , N = { x ∈ ℝ : − 2 ≤ x ≤ 1 } , P = { x ∈ ℝ : − 5 < x ≤ 0 } .
Mệnh đề nào sau đây là mệnh đề đúng?
A. M ⊂ N
B. M ⊃ P
C. N ⊂ M
D. N ⊂ P
Đáp án C.
Giải thích
M = x ∈ R : x ≥ - 3 = [ - 3 ; + ∞ ) N = x ∈ R : - 2 ≤ x ≤ 1 = [ - 2 ; 1 ] P = x ∈ R : - 5 < x ≤ 0 = ( - 5 ; 0 ]
Ta thấy rằng - 2 ; 1 ⊂ [ - 3 ; + ∞ ) d o đ ó N ⊂ M
Đúng 0
Bình luận (0)
Cho hàm số f (x) liên tục trên
ℝ
và
f
(
x
)
(
x
-
1
)
2
(
x
-
3
)
Mệnh đề nào dưới đây đúng? A. Hàm số không có cực trị B. Hàm số có hai điểm cực trị C. Hàm số có một điểm cực đại D. Hàm số có đúng một điểm cực trị
Đọc tiếp
Cho hàm số f (x) liên tục trên ℝ và f ' ( x ) = ( x - 1 ) 2 ( x - 3 ) Mệnh đề nào dưới đây đúng?
A. Hàm số không có cực trị
B. Hàm số có hai điểm cực trị
C. Hàm số có một điểm cực đại
D. Hàm số có đúng một điểm cực trị
Đáp án D
Ta thấy f'(x) =0 tại x=3,x=1 nhưng chỉ đổi dấu qua x = 3 nên hàm số có đúng 1 cực trị
Đúng 0
Bình luận (0)
Cho hàm số f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:Mệnh đề nào dưới đây là mệnh đề đúng? A. Hàm số có giá trị cực đại bằng 3. B. Hàm số có hai điểm cực trị. C. Hàm số có giá trị lớn nhất bằng 1, nhỏ nhất bằng -1/3. D. Đồ thị hàm số không cắt trục hoành.
Đọc tiếp
Cho hàm số f(x) xác định, liên tục trên ℝ và có bảng biến thiên như sau:
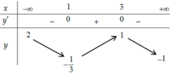
Mệnh đề nào dưới đây là mệnh đề đúng?
A. Hàm số có giá trị cực đại bằng 3.
B. Hàm số có hai điểm cực trị.
C. Hàm số có giá trị lớn nhất bằng 1, nhỏ nhất bằng -1/3.
D. Đồ thị hàm số không cắt trục hoành.
Có bao nhiêu mệnh đề sau là đúng?
1
6
x
≥
1
∀
x
∈
ℝ
2
x
2
2
x
-
1
∀
x
∈
ℝ
3
x
+
1...
Đọc tiếp
Có bao nhiêu mệnh đề sau là đúng?
1 6 x ≥ 1 ∀ x ∈ ℝ
2 x 2 > 2 x - 1 ∀ x ∈ ℝ
3 x + 1 > 2 x ∀ x ∈ ℝ
log 3 x 2 ≥ 0 ∀ x ≠ 0
a - b 2 a - 2 b ≥ 0 ∀ a , b ∈ ℝ
A. 2
B. 3
C. 4
D. 5
Hàm số y f(x) có đạo hàm
f
x
−
x
−
1
2
−
1
,
∀
x
∈
ℝ
.
Mệnh đề nào dưới đây đún...
Đọc tiếp
Hàm số y = f(x) có đạo hàm f ' x = − x − 1 2 − 1 , ∀ x ∈ ℝ . Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên ( − ∞ ; 1 ) .
B. Hàm số đồng biến trên (0;1)
C. Hàm số nghịch biến trên − ∞ ; + ∞ .
D. Hàm số đồng biến trên 1 ; + ∞ .
Đáp án C
Từ giả thiết em có f ' x = − x − 1 2 − 1 < 0 , ∀ x ∈ ℝ . Hàm số f(x) luôn nghịch biến trên − ∞ ; + ∞ .
Đúng 0
Bình luận (0)
Cho hàm số
y
f
(
x
)
liên tục trên
ℝ
và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau(1) Hàm số
y
f
(
x
)
đạt cực đại tại
x
0
0
(2) Hàm số
y
f
(
x
)
có ba cực trị.(3) Phương trình
y
f
(
x
)
có đúng ba nghiệm phân biệt(4) Hàm...
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên ℝ và có đồ thị như hình vẽ bên. Xét 4 mệnh đề sau
(1) Hàm số y = f ( x ) đạt cực đại tại x 0 = 0
(2) Hàm số y = f ( x ) có ba cực trị.
(3) Phương trình y = f ( x ) có đúng ba nghiệm phân biệt
(4) Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Hỏi trong 4 mệnh đề trên, có bao nhiêu mệnh đề đúng?
A. 1
B. 3
C. 4
D. 2
Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
Đúng 0
Bình luận (0)
Cho hàm số
f
x
0
,
x
∈
ℝ
,
f
0
1
,
f
x
f
x
.
x
+
1
,
∀
x
∈
ℝ
. Mệnh đề nào dưới đây đúng? A. f(3) 2 B. 2 f(3) 4 C. 4 f(3) 6 D. f(3) f(6)
Đọc tiếp
Cho hàm số f x > 0 , x ∈ ℝ , f 0 = 1 , f x = f ' x . x + 1 , ∀ x ∈ ℝ . Mệnh đề nào dưới đây đúng?
A. f(3) < 2
B. 2 < f(3) < 4
C. 4 < f(3) < 6
D. f(3) > f(6)
Cho hàm số f(x) liên tục trên
ℝ
và
f
x
x
−
1
2
x
−
3
.
Mệnh đề nào dưới đây đúng ? A. Hàm số không có cực trị B. Hàm số có hai điểm cự...
Đọc tiếp
Cho hàm số f(x) liên tục trên ℝ và f ' x = x − 1 2 x − 3 . Mệnh đề nào dưới đây đúng ?
A. Hàm số không có cực trị
B. Hàm số có hai điểm cực trị
C. Hàm số có một điểm cực đại
D. Hàm số có đúng một điểm cực trị
Đáp án D
Ta thấy f’(x) chỉ đổi dấu khi qua điểm x = 3 nên hàm số chỉ có 1 cực trị
Đúng 0
Bình luận (0)
Cho hàm số f(x)0 với
x
∈
ℝ
,
f
(
0
)
1
và
f
(
x
)
x
+
1
.
f
(
x
)
với mọi
x
∈
ℝ
. Mệnh đề nào dưới đây đúng?
Đọc tiếp
Cho hàm số f(x)>0 với x ∈ ℝ , f ( 0 ) = 1 và f ( x ) = x + 1 . f ' ( x ) với mọi x ∈ ℝ . Mệnh đề nào dưới đây đúng?
Cho hàm số
f
(
x
)
liên tục trên
ℝ
và
f
(
x
)
≠
0
với mọi
x
∈
ℝ
thỏa mãn
f
(
x
)
(
2
x
+
1
)
.
f
2
(
x...
Đọc tiếp
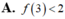
Cho hàm số f ( x ) liên tục trên ℝ và f ( x ) ≠ 0 với mọi x ∈ ℝ thỏa mãn f ' ( x ) = ( 2 x + 1 ) . f 2 ( x ) v à f ( 1 ) = - 0 , 5 . Biết tổng f ( 1 ) + f ( 2 ) + f ( 3 ) + . . . + f ( 2017 ) = a b ; ( a ∈ ℝ ; b ∈ ℝ ) v ớ i a b tối giản. Mệnh đề nào dưới đây đúng?
A. b - a = 4035
B. a + b = - 1
C. a b < - 1
D. a ∈ - 2017 ; 2017
