Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x = 1, x = 2, y = 0. Thể tích của khối tròn xoay thu được khi quay hình D xung quanh trục Ox bằng
![]()
![]()
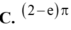
![]()
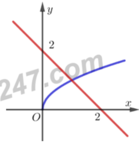
Cho hình phẳng giới hạn bởi đồ thị các hàm số y = x , đường thẳng y = 2 - x và trục hoành. Diện tích hình phẳng sinh bởi hình phẳng giới hạn bởi các đồ thị trên là
A. 7 6 .
B. 4 3 .
C. 5 6 .
D. 5 4 .
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a; x = b Diện tích S của hình phẳng D được tính theo công thức
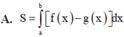
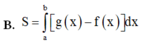
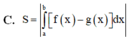
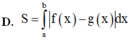
Cho hai hàm số y = f(x) và y = g(x) liên tục trên đoạn [ a; b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số đó và các đường thẳng x = a , x = b a < b . Diện tích S của hình phẳng D được tính theo công thức
A. S = ∫ a b f x − g x d x
B. S = ∫ a b g x − f x d x
C. S = ∫ a b f x − g x d x
D. S = ∫ a b f x − g x d x
Đáp án D
Phương pháp giải: Công thức tính diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
Lời giải:
Diện tích S của hình phẳng D được tính theo công thức là S = ∫ a b f x − g x d x
Cho hàm số y = f(x) liên tục trên đoạn [a;b] Gọi D là hình phẳng giới hạn bởi đồ thị hàm số y = f(x) trục hoành và hai đường thẳng x=a; x=b. Diện tích hình phẳng D được tính bởi công thức.
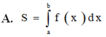
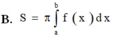
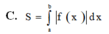
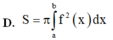
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = xe x và các đường thẳng x = 1 , x = 2 , y = 0 . Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
A. V = πe 2
B. V = 2 πe
C. V = ( 2 − e)π
D. V = 2 πe 2
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x = 1 , x = 2 , y = 0 . Thể tích của khối tròn xoay thu được khi quay hình D xung quanh trục Ox bằng
A. πe 2
B. 2 πe
C. 2 - e π
D. 2 πe 2
Gọi D là hình phẳng giới hạn bởi đồ thị của hàm số y = x e x và các đường thẳng x=1; x=2; y=0. Tính thể tích V của khối tròn xoay thu được khi quay hình D xung quanh trục Ox.
![]()
![]()
![]()
![]()
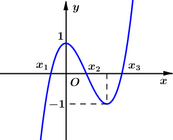
Cho hàm số bậc ba y=f(x) có đồ thị (C) như hình vẽ. Biết đồ thị hàm số đã cho cắt trục Ox tại 3 điểm có hoành độ
x
1
,
x
2
,
x
3
theo thứ tự lập thành cấp số cộng và
x
3
-
x
1
=
2
3
. Gọi diện tích hình phẳng giới hạn bởi (C) và trục Ox là S. Diện tích
S
1
của hình phẳng giới hạn bởi các đường
y
=
f
x
+
1
,
y
=
-
f
x
-
1
,
x
=
x
1
và
x
=
x
3
bằng![]()
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Biết đồ thị hàm số f ( x ) = a x 4 + b x 2 + c cắt trục hoành tại 4 điểm phân biệt. Gọi S 1 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm dưới trục hoành. Gọi S 2 là diện tích của hình phẳng giới hạn bởi trục hoành và phần đồ thị hàm số f ( x ) nằm phía trên trục hoành. Cho biết 5 b 2 = 36 a c . Tính tỉ số S 1 S 2
A. S 1 S 2 = 2 .
B. S 1 S 2 = 1 4 .
C. S 1 S 2 = 1 2 .
D. S 1 S 2 = 1 .
Đáp án D
Phương trình hoành độ giao điểm của đồ thị f ( x ) và Ox: a x 4 + b x 2 + c = 0 .
Để phương trình có bốn nghiệm
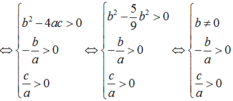
Gọi x 1 , x 2 , x 3 , x 4 lần lượt là bốn nghiệm của phương trình a x 4 + b x 2 + c = 0 và x 1 < x 2 < x 3 < x 4 . Không mất tính tổng quát, giả sử a > 0 .
Khi đó
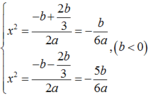
Suy ra x 1 = - - 5 b 6 a ; x 2 = - - b 6 a ; x 3 = - b 6 a ; x 4 = - b 6 a .
Do đồ thị hàm số f ( x ) nhận trục tung làm trục đối xứng nên ta có:
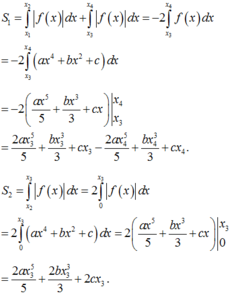
Suy ra
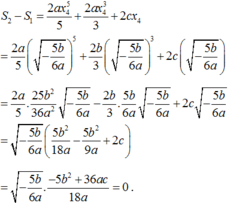
Vậy S 1 = S 2 hay S 1 S 2 = 1 .