Trong không gian Oxyz, cho hai mặt phẳng (P): 2x-2y+6z-3=0 (Q): x-y+3z-1=0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x – y + 3z – 1 = 0 và mặt phẳng (Q): 4x – 2y + 6z – 1 = 0. Trong các mệnh đề sau, mệnh đề nào đúng?
A. (P) và (Q) vuông góc với nhau
B. (P) và (Q) trùng nhau
C. (P) và (Q) cắt nhau
D. (P) và (Q) song song với nhau
Đáp án D
Phương pháp: Xét hai mặt phẳng
![]()
![]()
+ 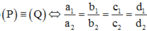 . Khi đó
n
(
P
)
→
/
/
n
Q
→
. Khi đó
n
(
P
)
→
/
/
n
Q
→
+ (P) và (Q) cắt nhau khi và chỉ khi chúng không song song hay trùng nhau
+ (P) ⊥ (Q) <=> n P → ⊥ n Q → ⇔ n P → . n Q → = 0
Cách giải: (P): 2x – y + 3z – 1 = 0; (Q): 4x – 2y + 6z – 1 = 0
Ta có: 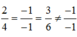
=> (P) và (Q) song song với nhau
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x-y+3z-1=0 và mặt phẳng (Q): 4x-2y+6z-1=0. Trong các mệnh đề sau, mệnh đề nào đúng?
A. (P) và (Q) vuông góc với nhau.
B. (P) và (Q) trùng nhau.
C. (P) và (Q) cắt nhau.
D. (P) và (Q) song song với nhau.
Đáp án D
Phương pháp: Xét hai mặt phẳng
![]()
![]()
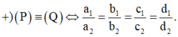
![]()
+) (P) và (Q) cắt nhau khi và chỉ khi chúng không song song hay trùng nhau.
![]()
Cách giải: Ta có: (P): 2x-y+3z-1=0 và (Q): 4x-2y+6z-1=0
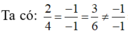
=> (P) và (Q) song song với nhau.
Trong không gian Oxyz, cho mặt phẳng (P): x - 2y + 3z + 1 = 0 và mặt cầu (S): x 2 + y 2 + z 2 - 2x - 4y + 6z + 5 = 0. Khẳng định nào dưới đây là đúng?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Cả ba khẳng định trên đều sai
Đáp án A
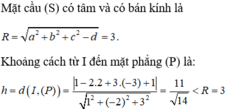
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn.
Trong không gian Oxyz, cho mặt cầu (S) có phương trình là x2 + y2 + z2 - 2x - 4y + 6z + 5 = 0 và cho mặt phẳng (P) : x - 2y + 3z + 3 = 0. Khẳng định nào dưới đây là đúng ?
A. (P) giao (S) theo một đường tròn
B. (P) tiếp xúc với (S)
C. (P) không cắt (S)
D. Mặt phẳng (P) đi qua tâm của mặt cầu (S)
Đáp án A
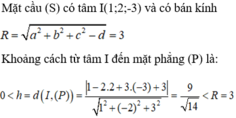
Do đó mặt phẳng (P) giao với mặt cầu (S) theo một đường tròn và (P) không đi qua tâm I của (S).
Vậy đáp án đúng là A.
Trong không gian Oxyz , cho hai mặt phẳng (P) 2x-my+3z+6+m=0, (Q) (m+3)x-2y+(5m+1)-10=0. Tìm giá trị thực của m để mặt phẳng (P) vuông góc với (Q)
A. m=1
B. m = - 9 19
C. m ≠ 1
D. m = - 5 2
Trong không gian tọa độ Oxyz, cho mặt phẳng (P): 2x - 2y + z - 4 = 0 và mặt phẳng (Q): x + y - 3z - 5 = 0 . Gọi là góc giữa hai mặt phẳng và . Khẳng định nào sau đây là đúng?
![]()
![]()
![]()
![]()
Chọn A
Gọi φ là góc giữa hai mặt phẳng (P) và (Q)
Khi đó
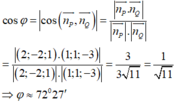
Trong không gian tọa độ Oxyz, cho mặt phẳng P : 2 x - 2 y + z - 4 = 0 và mặt phẳng Q : x + y - 3 z - 5 = 0 . Gọi φ là góc giữa hai mặt phẳng P và Q . Khẳng định nào sau đây là đúng?
A. φ ≈ 72 ° 27 '
B. φ ≈ 36 ° 28 '
C. P ⊥ Q
D. (P)//(Q)
Đáp án A
Gọi φ là góc giữa hai mặt phẳng P và Q .
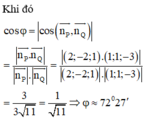
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M ( - 1 ; - 2 ; 5 ) và vuông góc với hai mặt phẳng ( Q ) : x + 2 y - 3 z + 1 = 0 v à ( R ) : 2 x - 3 y + z + 1 = 0 .
A. x- y + z – 6 = 0
B. x + y - z + 8 = 0
C. –x + y + z – 4 = 0
D. x + y + z - 2 = 0
Chọn D
![]()
![]()
![]()
nên mặt phẳng (P) nhận
![]()
và (P) đi qua điểm M(-1;-2;5) nên có phương trình là:
1 ( x + 1 ) + 1 ( y + 2 ) + 1 ( z - 5 ) = 0 h a y x + y + z - 2 = 0 .
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M ( - 1 ; - 2 ; 5 ) và vuông góc với hai mặt phẳng ( Q ) : x + 2 y - 3 z + 1 = 0 v à ( R ) : 2 x - 3 y + z + 1 = 0 .
A. x- y + z – 6 = 0
B. x + y - z + 8 = 0
C. –x + y + z – 4 = 0
D. x + y + z - 2 = 0
Chọn D
![]()
![]()
![]()
nên mặt phẳng (P) nhận
![]()
và (P) đi qua điểm M(-1;-2;5) nên có phương trình là:
1 ( x + 1 ) + 1 ( y + 2 ) + 1 ( z - 5 ) = 0 h a y x + y + z - 2 = 0 .