Cho hàm số y = f(x) có bảng biến thiên như sau
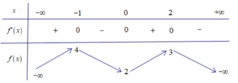
Bất phương trình x 2 + 1 f ( x ) ≥ m có nghiệm trên khoảng (-1;2) khi và chỉ khi
A. m<10
B. m ≤ 15
C. m<27
D. m<15
Cho hàm số y= f(x) Hàm số y= f’(x) có bảng biến thiên như sau
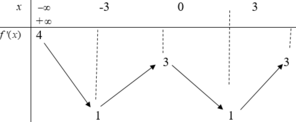
Bất phương trình f ( x ) < 3 e x + 2 + m có nghiệm x ∈ ( - 2 ; 2 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y=f(x) . Hàm số y= f'(x) có bảng biến thiên như sau

Bất phương trình f ( x ) < ln x + m đúng với mọi x ∈ ( 0 ; 1 ) khi và chỉ khi
A. I = l a a
B. I = l a
C. I = l a ( a - 1 )
D. I = l a ( a + 1 )
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
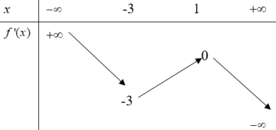
Bất phương trình
m
+
e
f
(
x
)
<
e
x
có nghiệm ![]() khi và chỉ khi
khi và chỉ khi
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x). Hàm số y = f'(x) có bảng biến thiên như sau
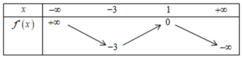
Bất phương trình f ( x ) < e x + m đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
![]()
![]()
![]()
![]()
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
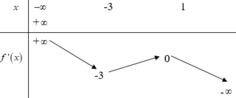
Bất phương trình f ( x ) < e x + m đúng với mọi x ∈ ( - 1 ; 1 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau
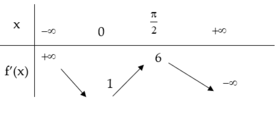 Bất phương trình
f
x
>
2
cos
x
+
3
m
đúng với mọi
x
∈
0
;
π
2
khi
Bất phương trình
f
x
>
2
cos
x
+
3
m
đúng với mọi
x
∈
0
;
π
2
khi
A. m ≤ 1 3 f 0 - 2
B. m < 1 3 f 0 - 2
C. m ≤ 1 3 f π 2 - 1
D. m < 1 3 f π 2 - 1
Cho hàm số y=f(x) Hàm số y=f '(x) có bảng biến thiên như sau
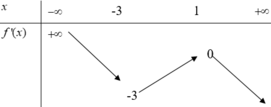
Bất phương trình m + e f ( x ) < e x có nghiệm x ∈ - 1 ; 1 khi và chỉ khi
A. m < 1 e - e f ( - 1 )
B. m ≤ 1 e - e f ( 1 )
C. m ≤ 1 e - e f ( - 1 )
D. m < e - e f ( 1 )
Bất phương trình tương đương với: ![]()
Ta có ![]() vì
vì ![]()
Do đó ![]()
![]()
Vậy (1) có nghiệm trên khoảng ![]()
Chọn đáp án D.
Cho hàm số y= f(x).Hàm số y= f’(x) có bảng biến thiên như sau
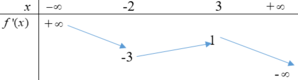
Bất phương trình f ( e x ) < e x + m nghiệm đúng với mọi x ∈ ( - 1 ; 1 ) khi và chỉ khi
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y = f (x). Hàm số y = f '(x) có bảng biến thiên như sau
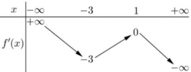
Bất phương trình f x < e x + m đúng với mọi x ∈ (-1;1) khi và chỉ khi
A. m ≥ f 1 - e
B. m > f - 1 - 1 e
C. m ≥ f - 1 - 1 e
D. m > f 1 - e
Cho hàm số y=f(x). Hàm số y=f'(x) có bảng biến thiên như sau:
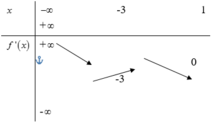
Bất phương trình f x < e x + m đúng với mọi x ∈ - 1 ; 1 khi và chỉ khi
A. m ≥ f 1 - e
B. m > f - 1 - 1 e
C. m ≥ f - 1 - 1 e
D. m > f 1 - e