Cho số phức z = ( 2 + i)( 3 - i) Tìm phần thực a và phần ảo b của số phức z ¯
A. a = 7 ; b = 1.
B. a = 7 ; b = -1.
C. a = - 7; b = 1.
D. a = -7; b = - 1.
Chọn B.
Ta có: z = ( 2 + i) ( 3 - i) = 6 - 2i + 3i - i2 = 7 + i
Nên 
vậy phần thực bằng a = 7 và phần ảo b = -1.
Cho số phức z = 4 - 8 i 1 + i . Tìm phần thực a và phần ảo b của số phức z ¯
A. a = 2; b = 6.
B. a = -2; b = -6.
C. a = -2; b = 6.
D. a = 2; b = -3.
Chọn C.
Theo giả thiết ta có:
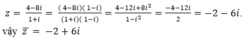
⇒ Phần thực a = -2 và phần ảo bằng b = 6.
Cho số phức z = 1 - i + i 3 . Tìm phần thực a và phần ảo b của z
A. a = 1; b = -2
B. a = -2; b = 1
C. a = 1; b = 0
D. a = 0; b = 1
Tìm phần thực a và phần ảo b của số phức z, biết 2 - i 1 + i + z ¯ = 4 - 2 i
A. a = - 1 , b = 3
B. a = 1 , b = 3
C. a = - 3 , b = 1
D. a = - 3 , b = - 1
Cho hai số phức z 1 = 7 + 9 i và z 2 = 8 i . Gọi z = a + b i a , b ∈ ℝ là số phức thỏa mãn z − 1 − i = 5 . Tìm a+b, biết biểu thức P = z − z 1 + 2 z − z 2 đạt giá trị nhỏ nhất.
A. ‒3
B. ‒7
C. 3
D. 7
Cho hai số phức z 1 = 7 + 9 i và z 2 = 8 i . Gọi z = a + b i a , b ∈ ℝ là số phức thỏa mãn z − 1 − i = 5 . Tìm a + b , biết biểu thức P = z − z 1 + 2 z − z 2 đạt giá trị nhỏ nhất
A. ‒3
B. ‒7
C. 3
D. 7
Đáp án D.
Gọi M a ; b là điểm biểu diễn số phức z = a + b i . Đặt I = 1 ; 1 , A 7 ; 9 và B 0 ; 8
Ta xét bài toán: Tìm điểm M thuộc đường tròn C có tâm I, bán kính R = 5 sao cho biểu thức P = M A + 2 M B đạt giá trị nhỏ nhất.
Trước tiên, ta tìm điểm K x ; y sao cho M A = 2 M K ∀ M ∈ C .
Ta có
M A = 2 M K ⇔ M A 2 = 4 M K 2 ⇔ M I → + I A → 2 = 4 M I → + I K → 2
⇔ M I 2 + I A 2 + 2 M I → . I A → = 4 M I 2 + I K 2 + 2 M I → . I K →
⇔ 2 M I → I A → − 4 I K → = 3 R 2 + 4 I K 2 − I A 2 *
(*) luôn đúng ∀ M ∈ C ⇔ I A → − 4 I K → = 0 → 3 R 2 + 4 I K 2 − I A 2 = 0 .
I A → − 4 I K → = 0 → ⇔ 4 x − 1 = 6 4 y − 1 = 8 ⇔ x = 5 2 y = 3
Thử trực tiếp ta thấy K 5 2 ; 3 thỏa mãn 3 R 2 + 4 I K 2 − I A 2 = 0 .
Ta cos M A + 2 M B = 2 M K + 2 M B = 2 M K + M B ≥ 2 K B .
Vì B I 2 = 1 2 + 7 2 = 50 > R 2 = 25 nên B nằm ngoài (C).
Vì K I 2 = 3 2 2 + 2 2 < R 2 = 25 nên K nằm trong (C) .
Dấu bằng trong bất đẳng thức trên xảy ra khi và chỉ khi M thuộc đoạn thẳng BK . Do đó M A + 2 M B nhỏ nhất khi và chỉ khi M là giao điểm của (C) và đường thẳng BK.
Phương trình đường thẳng B K : 2 x + y − 8 = 0 .
Phương trình đường tròn C : x − 1 2 + y − 1 2 = 25 .
Tọa độ điểm M là nghiệm của hệ
2 x + y = 8 x − 1 2 + y − 1 2 = 25 ⇔ x = 1 y = 6
hoặc x = 5 y = − 2 .
Thử lại thấy M 1 ; 6 thuộc đoạn BK.
Vậy a = 1, b = 6 ⇒ a + b = 7 .
Cho số phức z thỏa mãn 5 z + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a+b bằng
A. 13
B. -5
C. 9
D. 5
Cho số phức z thỏa mãn 5 z ¯ + i = 2 - i z + 1 . Gọi a, b lần lượt là phần thực và phần ảo của số phức 1 + z + z 2 , tổng a + b bằng
A. 13
B. -5
C. 9
D. 5
Cho hai số phức:
z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ ) .
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' − a ' b
D. a a ' − b b '
Đáp án A.
Có z . z ' = a a ' − b b ' + a b ' + a ' b i .
Vậy phần ảo là: a b ' + b a ' i .
Cho hai số phức z = a + b i , z ' = a ' + b ' i ( a , b , a ' , b ' ∈ ℝ )
Tìm phần ảo của số phức z z ' .
A. ( a b ' + a ' b ) i
B. a b ' + a ' b
C. a b ' - a ' b
D. a a ' - b b '
Đáp án A.
Có 
.
Vậy phần ảo là (ab'+ba')i.
