Trong không gian với hệ tọa độ Oxyz cho tam giác ABC biết A 2 ; 1 , 0 ; B 3 , 0 , 2 ; C 4 , 3 , - 4 . Viết phương trình đường phân giác trong góc A.
A. x = 2 y = 1 + t z = 0
B. x = 2 y = 1 z = t
C. x = 2 + t y = 1 z = 0
D. x = 2 + t y = 1 z = t
Những câu hỏi liên quan
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết
A
(
3
;
1
;
2
)
,
B
(
1
;
−
4
;
2
)
,
C
(
2
;
0
;
−
1
)
.
Tìm tọa độ tâm G của tam giác ABC A. G (2;-1;1). B. G (6;-3;3). C. G (2;1;1). D. G (2;-1;3).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho tam giác ABC biết A ( 3 ; 1 ; 2 ) , B ( 1 ; − 4 ; 2 ) , C ( 2 ; 0 ; − 1 ) . Tìm tọa độ tâm G của tam giác ABC
A. G (2;-1;1).
B. G (6;-3;3).
C. G (2;1;1).
D. G (2;-1;3).
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;2;-1), B(2;-1;3), C(-4;7;5). Tọa độ chân đường phân giác trong góc
B
^
của tam giác ABC là A.
-
2
3
;
11
3
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;2;-1), B(2;-1;3), C(-4;7;5). Tọa độ chân đường phân giác trong góc B ^ của tam giác ABC là
A. - 2 3 ; 11 3 ; 1
B. 11 3 ; - 2 ; 1
C. 2 3 ; 11 3 ; 1 3
D. (-2;11;1)
Đáp án A
Gọi D là chân đường phân giác góc B của tam giác ABC . Theo tính chất đường phân giác ta có :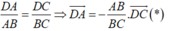 
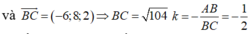
Từ (*) ta có, điểm D chia đoạn thẳng AC theo tỷ số k nên D có toạ độ
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với
A
-
1
;
4
;
1
,
B
1
;
1
;
-
6
,
C
0
;
-
2...
Đọc tiếp
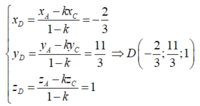
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A - 1 ; 4 ; 1 , B 1 ; 1 ; - 6 , C 0 ; - 2 ; 3 . Tìm tọa độ trọng tâm G của tam giác ABC.
A. G - 1 2 ; 5 2 ; - 5 2
B. G - 1 ; 3 ; - 2
C. G 1 3 ; - 1 ; 2 3
D. G - 1 3 ; 1 ; - 2 3
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC A.
G
-
1
3
;
1
;
-
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC
A. G - 1 3 ; 1 ; - 2 3
B. G - 1 ; 3 ; - 2
C. G 1 3 ; - 1 ; 2 3
D. G - 1 2 ; 5 2 ; - 5 2
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC. A.
G
-
1
3
;
1
;
-
2
3
B. G(-1;3;-2) C. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC với A(-2;4;1), B(1;1;-6), C(0;-2;3). Tìm tọa độ trọng tâm G của tam giác ABC.
A. G - 1 3 ; 1 ; - 2 3
B. G(-1;3;-2)
C. G 1 3 ; - 1 ; 2 3
D. G - 1 2 ; 5 2 ; - 5 2
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC. A. G(3;3;3) B. G(1;1;1) C. G(2/3;2/3;2/3) D. G(1/3;1/3;1/3).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(3;0;0), B(0;3;0) và C(0;0;3). Tìm tọa độ trọng tâm G của tam giác ABC.
A. G(3;3;3)
B. G(1;1;1)
C. G(2/3;2/3;2/3)
D. G(1/3;1/3;1/3).
Đáp án B
Tọa độ trọng tâm tam giác ABC là G(1;1;1).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có
A
(
1
;
−
1
;
0
)
,
B
(
2
;
3
;
1
)
,
C
(
3
;
1
;
−
4
)
. Tọa độ tâm G của tam giác ABC là A. G(6;3;-3) B. G(4;2;-2) C. G(-2;-1;1) D. G(2;1;-1)
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC có A ( 1 ; − 1 ; 0 ) , B ( 2 ; 3 ; 1 ) , C ( 3 ; 1 ; − 4 ) . Tọa độ tâm G của tam giác ABC là
A. G(6;3;-3)
B. G(4;2;-2)
C. G(-2;-1;1)
D. G(2;1;-1)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;0), B(0;0;1) và C(2;1;1). Tìm tổng tọa độ trực tâm H của tam giác ABC. A. 1 B. 2 C. 0 D. Không có điểm H
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;0), B(0;0;1) và C(2;1;1). Tìm tổng tọa độ trực tâm H của tam giác ABC.
A. 1
B. 2
C. 0
D. Không có điểm H
Đáp án A
- Cách 1: Giả sử H(x;y;z) là trực tâm của tam giác ABC, ta có điều kiện sau:
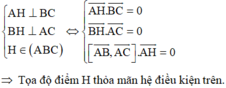
Do nhận xét được AB → . AC → = 0 ⇒ AB → ⊥ AC → nên ta tìm được cách giải độc đáo sau:
- Cách 2: Vì tam giác ABC vuông tại A nên trực tâm H của tam giác ABC trùng với điểm A
- Lời giải chi tiết cho cách 2: AB → = − 1 ; 0 ; 1 ; AC → = 1 ; 1 ; 1 , nhìn nhanh thấy
AB → . AC → = 0 ⇒ AB ⊥ AC nên tam giác ABC vuông tại A và A là trực tâm
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;0), B(0;0;1), C(2;1;1). Diện tích tam giác ABC bằng A.
11
2
B.
7
2
C.
6
2
D.
5
2
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có A(1;0;0), B(0;0;1), C(2;1;1). Diện tích tam giác ABC bằng
A. 11 2
B. 7 2
C. 6 2
D. 5 2
