Hình vẽ bên là đồ thị của hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e .
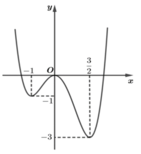
Hỏi có bao nhiêu m nguyên để phương trình f x = m có ít nhất ba nghiệm phân biệt?
A. 1.
B. 2.
C. 3.
D. 4.
Hàm số y=f(x) có đồ thị như hình vẽ bên. Hình nào dưới đây là đồ thị của hàm số y=|f(x)|
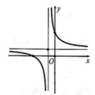
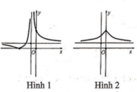
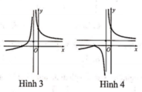
A. Hình 1
B. Hình 2
C. Hình 3
D. Hình 4
Hàm số y=f(x) có đồ thị như hình vẽ bên. Điểm cực tiểu của đồ thị hàm số y=f(x) là
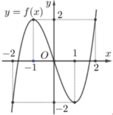
A. 1
B. (1;-2)
C. -1
D. (-1;2)
Điểm cực tiểu của đồ thị hàm số là (1;−2).
Chọn đáp án B.
Hình vẽ bên là đồ thị của hàm số y=f(x). Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y=f(x) là
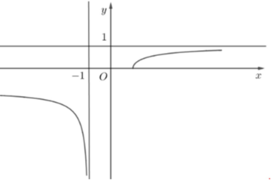
A. x=-1; y=1
B. x=1; y=-1
C. x=-1; y=-1
D. x=1; y=1
Quan sát đồ thị có ![]()
![]() là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho.
Chọn đáp án A.
Cho hàm số f ( x ) = a x 4 + b x 2 - 1 ( a , b ∈ ℝ ) . Đồ thị của hàm số y=f(x) như hình vẽ bên. Số nghiệm thực của phương trình 2018.f(x) + 2019 = 0 là:
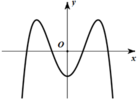
A. 4
B. 0
C. 3
D. 2
Cho đồ thị hàm số y = 1 2 ( x - 1 ) ( x 2 - 4 ) như hình vẽ bên. Số điểm cực trị của đồ thị hàm số f(x)=|(|x-1| ( x 2 - 4 ) +m)| , với m thuộc đoạn (2;6) là
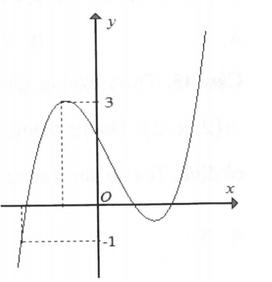
A. 6.
B. 3.
C. 7.
D. 5.
Cho đồ thị hàm số
y
=
1
2
(
x
-
1
)
(
x
2
-
4
)
như hình vẽ bên. Số điểm cực trị của đồ thị hàm số
f
(
x
)
=
x
-
1
(
x
2
-
4
)
+
m
, với m thuộc đoạn (2;6) là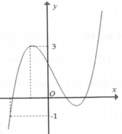
![]()
![]()
![]()
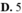
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1 đường thẳng △ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2 Tích phân ∫ 0 ln 3 e x f ' ' e x + 1 2 d x bằng
A. 8
B. 4
C. 3
D. 6
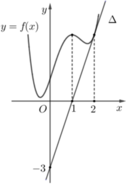
Cho hàm số f(x) có đạo hàm cấp hai f''(x) liên tục trên R và có đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x = 1 đường thẳng ![]() trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 . Tích phân
∫
0
ln
3
e
x
f
"
e
x
+
1
2
d
x
bằng
A. 8
B. 4
C. 3
D. 6
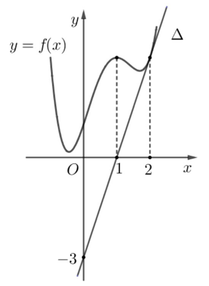
Cho hàm số f(x) có đạo hàm cấp hai f'''(x) liên tục trên R và đồ thị hàm số f(x) như hình vẽ bên. Biết rằng hàm số f(x) đạt cực đại tại điểm x=1; đường thẳng ∆ trong hình vẽ bên là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x=2. Tích phân ∫ 0 ln 3 e x f ' ' ( e x + 1 2 ) d x bằng
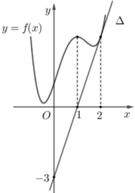
A. 8
B. 4
C. 3
D. 6
Chọn đáp án D
![]()
![]()
![]()
![]()
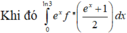
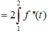

![]()
Do hàm số đạt cực đại tại điểm x=1⇒ f′(1) = 0 và đường thẳng Δ qua hai điểm (0;−3);(1;0) nên có phương trình y=3x−3.
Vì Δ là tiếp tuyến của đồ thị hàm số f(x) tại điểm có hoành độ x = 2 ⇒ f ' ( 2 ) = k △ =3
Vậy
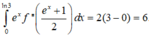
Cho hàm số f(x) có đồ thị f'(x) như hình vẽ bên. Số điểm cực trị của hàm số f(x) là
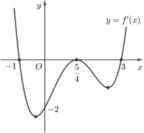
A. 3.
B. 4.
C. 2.
D. 1.