Kí hiệu  x 1 ,   x 2 là hai nghiệm thực của phương trình  4 x 2 - x   +   2 x 2 - x + 1   =   3 Giá trị  x 1   -   x 2 là

A.3

B.2

C.4

D.1

Kí hiệu x = - a b là một nghiệm của phương trình 1 + log 6 x - 1 x + 7 = 1 2 log 6 x - 1 2 với a b  là số tự nhiên có hai chữ số. Tính tổng a + 2b

A. 4

B. 5

C. 7

D. 9

Kí hiệu F(x) là một nguyên hàm của hàm số f ( x )   =   1 e x + 1 , biết F(0) = -ln2. Tìm tập nghiệm S của phương trình

A. S = {-3;3}

B. S = {3}

C.  S   =   ∅

D. S = {-3}

Kí hiệu F (x) là một nguyên hàm của hàm số f ( x ) = 1 e x + 1 , biết F 0 = - ln 2 . Tìm tập nghiệm S của phương trình F ( x ) + ln ( e x + 1 ) = 3 .

A.  S = - 3 ; 3

B.  S = 3

C.  S = ∅

D.  S = - 3

Kí hiệu là hai nghiệm phức của phương trình 3 z 2   -   z   +   1   =   0  .Tính P = z 1   +   z 2  

A .   P   =   14 3

B .   P   =   2 3

C .   P   =   3 3

D .   P   =   2 3 3

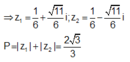
Cho phương trình  ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x   4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt

A. 3.

B. 4.

C. 5.

D. 6

Kí hiệu  z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 1 = 0 . Tính  | z 1 | + | z 2 | .

A. 1/3.

B.  3 3

C.  2 3 3

D. 3

Kí hiệu z₁, z₂ là hai nghiệm phức của phương trình z 2 + z + 2 = 0  Tính  z 1 z 2 + z 2 z 1