Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a 21 6 tính theo a thể tích V của hình chóp đã cho
A. V = a 3 3 8
B. V = a 3 3 6
C. V = a 3 3 12
D. V = a 3 3 24
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng 3a. Thể tích khối chóp S.ABC tính theo a là:
A. 26 a 3 12
B. 78 a 3 12
C. 26 a 3 3
D. 78 a 3 3
Đáp án A
Gọi H là hình chiếu của S lên (ABCD)
Ta có: A H = a 2 − a 2 2 = a 3 3 ;
S H = 3 a 2 − a 3 3 2 = 26 3 a
Thể tích khối chóp là:
V = 1 3 S H . S A B C D = 1 3 . 26 3 a . 1 2 a 2 sin 60 ° = 26 a 3 12
Cho hình chóp đều S.ABC có cạnh đáy bằng a, cạnh bên bằng a 21 6 , tính theo a thể tích V của hình chóp đã cho
A. V = a 3 3 8
B. V = a 3 3 6
C. V = a 3 3 12
D. V = a 3 3 24
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60 ° . Tính theo a thể tích V của khối chóp S.ABC
A. V = a 3 3 4
B. V = a 3 3 12
C. V = a 3 12
D. V = a 3 3 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a, góc giữa cạnh bên và mặt đáy bằng 60°. Tính theo a thể tích V của khối chóp S.ABC.
A. V = a 3 3 24
B. V = a 3 3 12
C. V = a 3 12
D. V = a 3 3 3
Chọn B
Gọi H là trọng tâm tam giác ABC, khi đó
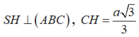
Góc giữa cạnh bên và mặt đáy là góc
![]()

Cho hình chóp đều S.ABC có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60 o . Tính theo thể tích khối chóp S.ABC.
A. V = a 3 3 24
B. V = a 3 8
C. V = a 3 3 12
D. V = a 3 3 8
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , cạnh bên tạo với đáy góc 60 0 . Tính theo a thể tích khối chóp S.ABC?
A. 2 a 3 3 3
B. a 3 3 3
C. a 3 3 4
D. a 3 3
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng 2a , cạnh bên tạo với đáy góc 60 0 . Tính theo a thể tích khối chóp S.ABC ?
A. 2 a 3 3 3
B. a 3 3 3
C. a 3 3 4
D. a 3 3
Đáp án là A
Ta có:
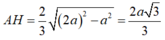
Theo giả thiết cạnh bên tạo đáy góc 60 0 suy ra góc SAH= 60 0
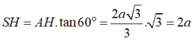
là tam giác đều cạnh 2a nên diện tích là
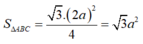
Thể tích khối chóp S.ABC là
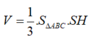
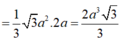
Cho hình chóp đều có cạnh đáy bằng a, góc giữa mặt bên và đáy bằng 60 ° . Tính theo thể tích khối chóp S.ABC.
A. V = a 3 3 24
B. V = a 3 8
C. V = a 3 3 12
D. V = a 3 3 8
Phương pháp:
+ Sử dụng định nghĩa để tìm góc giữa hai mặt phẳng (P) và (Q):
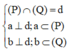 khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
khi đó góc giữa (P) và (Q) chính là góc giữa hai đường thẳng a và b.
+ Diện tích tam giác đều cạnh a được tính theo công thức S = a 2 3 4
+ Tính thể tích V = 1 3 S.h với S là diện tích đáy, h là chiều cao hình chóp.
Cách giải:
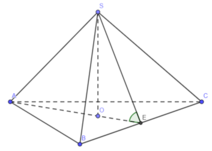
Gọi E là trung điểm của BC, O là trọng tâm tam giác ABC => SO ⊥ (ABCD) (do S.ABC là hình chóp đều)
Suy ra AE ⊥ BC (do ∆ ABC đều) và SE ⊥ BC (do ∆ SBC cân tại S)
Ta có 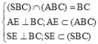 nên góc giữa (ABC) và (SBC) là SEA.
nên góc giữa (ABC) và (SBC) là SEA.
Từ giả thiết suy ra SEA = 60 ° .
Tam giác ABC đều cạnh a ![]()
Xét tam giác SOE vuông tại O (do SO ⊥ (ABC)=> SO ⊥ AE), ta có:
![]()
Diện tích tam giác đều ABC là: ![]()
Vậy 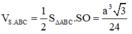
Chọn A
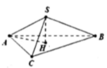
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a 3 và cạnh bên bằng 2a. Thể tích khối chóp S.ABC theo a là?
A. a 3 3 6
B. a 3 3 3
C. a 3 3 4
D. 3 a 3 4
Đáp án: D
Hướng dẫn giả:
Gọi H là tâm của tam giác ABC
![]()
![]()
⇒ V S . A B C D = S H . S A B C 3 = 3 a 3 4 .