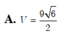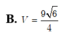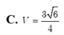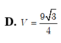Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết SC =a 3
A. a 3 6 12
B. 2 a 3 6 9
C. a 3 3 2
D. a 3 3 4
Những câu hỏi liên quan
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên (SAB), (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết
S
C
a
3
. A.
a
3
3
2
B.
a
3
3
4...
Đọc tiếp
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a và hai mặt bên (SAB), (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết S C = a 3 .
A. a 3 3 2
B. a 3 3 4
C. 2 a 3 6 9
D. a 3 6 12
Đáp án D
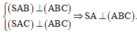
Xét tam giác SAC vuông tại A nên:
Đúng 0
Bình luận (0)
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết
S
C
a
3
A.
a
3
6
12
B.
2
a
3
6
9...
Đọc tiếp
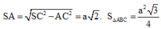
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết S C = a 3
A. a 3 6 12
B. 2 a 3 6 9
C. a 3 3 2
D. a 3 3 4
Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt (SAB) và(SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết
S
C
a
3
? A.
2
a
3
6
9
B....
Đọc tiếp
Cho khối chóp S.ABC có đáy là tam giác ABC đều cạnh a. Hai mặt (SAB) và(SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết S C = a 3 ?
A. 2 a 3 6 9
B. a 3 6 12
C. a 3 3 4
D. a 3 3 2
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết SC a
3
? A.
2
a
3
6
9
B.
a
3
6
12
C....
Đọc tiếp
Cho khối chóp S.ABC có đáy là tam giác đều cạnh a. Hai mặt (SAB) và (SAC) cùng vuông góc với đáy. Tính thể tích khối chóp biết SC = a 3 ?
A. 2 a 3 6 9
B. a 3 6 12
C. a 3 3 4
D. a 3 3 12
Phương pháp:
Sử dụng kiến thức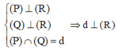 
để tìm chiều cao của hình chóp
Sử dụng công thức tính diện tích tam giác đều cạnh a là S = a 2 3 4
Sử dụng công thức tính thể tích khối chóp V = 1 3 S.h với S là diện tích đáy và h là chiều cao hình chóp.
Cách giải:
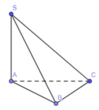
Từ đề bài ta có
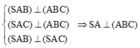
Vì tam giác đều cạnh a 
và AB = AC = BC = a.
Tam giác vuông tại A (do SA ⊥ (ABC) => SA ⊥ AC) nên theo định lý Pytago ta có
Thể tích khối chóp là 
Chọn B
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy và
S
B
a
3
. Tính thể tích khối chóp S.ABC A.
a
3
6
3
B.
a
3...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy và S B = a 3 . Tính thể tích khối chóp S.ABC
A. a 3 6 3
B. a 3 6 12
C. a 3 6 3
D. 2 a 3 6 9
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy và SB
a
3
. Tính thể tích khối chóp S.ABC. A.
a
3
6
3
B.
a
3
6
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hai mặt bên (SAB) và (SAC) cùng vuông góc với đáy và SB = a 3 . Tính thể tích khối chóp S.ABC.
A. a 3 6 3
B. a 3 6 12
C. a 3 6 3
D. 2 a 3 6 9
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc bằng 450. Thể tích của khối chóp S.ABC, tính theo a, là: A.
V
3
12
a
3
B.
V
1
3
a
3
C.
V
2
12...
Đọc tiếp
Cho khối chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt đáy và cạnh bên SC tạo với mặt đáy một góc bằng 450. Thể tích của khối chóp S.ABC, tính theo a, là:
A. V = 3 12 a 3
B. V = 1 3 a 3
C. V = 2 12 a 3
D. V = 1 6 a 3
Đáp án A
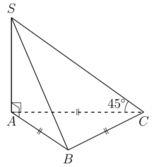
Từ giả thiết, ta suy ra góc giữa SC và mặt đáy chính là góc SCA. Suy ra tam giác SAC vuông cân ở A, và SA=AC=a.
Thể tích khối chóp là
V = 1 3 S A B C = 1 3 . 3 4 a 2 . a = 3 12 a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng A.
3
2
B.
3
4
C.
3
6
D.
3
12
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Gọi H là hình chiếu vuông góc của A lên SC. Biết . Thể tích của khối chóp S.ABC bằng
A. 3 2
B. 3 4
C. 3 6
D. 3 12
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), gọi M là điểm thuộc cạnh SC sao cho MC 2MS. Biết AB 3, BC
3
3
. Tính thể tích của khối chóp S.ABC
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, mặt bên (SAB) là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), gọi M là điểm thuộc cạnh SC sao cho MC = 2MS. Biết AB = 3, BC = 3 3 . Tính thể tích của khối chóp S.ABC
