Số mặt phẳng đối xứng của hình lập phương là:
A. 3.
B. 6.
C. 8.
D. 9.
Những câu hỏi liên quan
Số mặt phẳng đối xứng của hình lập phương là
A.6
B.7
C.8
D.9
Số mặt phẳng đối xứng của hình lập phương là:
A. 6
B. 7
C. 8
D. 9
Số mặt phẳng đối xứng của hình lập phương A B C D . A ' B ' C ' D ' là
A. 3
B. 6
C. 9
D. 12
Số mặt phẳng đối xứng của hình lập phương là ?
Xét khối lập phương ABCD.
Gọi M,N,P,Q lần lượt là trung điểm của AB, BC, CD, DA
R,S,T,U lần lượt là trung điểm của AA, BB, CC, DD
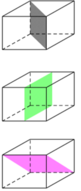
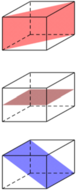
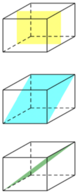
Khối lập phương ABCD có 9 mặt phẳng đối xứng như sau:
a) 3 mặt phẳng đối xứng chia nó thành hai khối hộp chữ nhật( là các mặt phẳng MPPM, NQQN, RSTU.
b) 6 mặt phẳng đối xứng chia nó thành hai khối lăng trụ tam giác( là các mặt phẳng ACCA, BDDB, ABCD, ABCD, ABCD, ABCD.
Đúng 0
Bình luận (0)
Gọi n là số mặt phẳng đối xứng của hình lập phương. Tìm n.
Số mặt phẳng đối xứng xủa hình lập phương là:
A. 3
B. 6
C. 8
D. 9
Chọn D.
Hình lập phương có 9 mặt phẳng đối xứng
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 0 và đường tròn (C) có phương trình:
x
2
+
y
2
+
2
x
−
6
y
+
6
0
.Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đườn...
Đọc tiếp
Trong mặt phẳng Oxy, cho hai điểm I(1; 2), M(-2; 3), đường thẳng d có phương trình 3x – y + 9 = 0 và đường tròn (C) có phương trình: x 2 + y 2 + 2 x − 6 y + 6 = 0 .
Hãy xác định tọa độ của điểm M’, phương trình của đường thẳng d’ và đường tròn (C’) theo thứ tự là ảnh của M, d và (C) qua
a) Phép đối xứng qua gốc tọa độ;
b) Phép đối xứng qua tâm I.
a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.
Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :
M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2 + y 2 − 2 x + 6 y + 6 = 0 .
b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .
Vì I là trung điểm của MM' nên M′ = (4;1)
Vì d' song song với d nên d' có phương trình 3x – y + C = 0.
Lấy một điểm trên d, chẳng hạn N(0; 9).
Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).
Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.
Vậy phương trình của d' là 3x – y – 11 = 0.
Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),
bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).
Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x − 3 2 + y − 1 2 = 4 .
Đúng 0
Bình luận (0)
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
là diện tích 6 mặt của hình lập phương,
S
2
là diện tích xung quanh của hình trụ. Tỉ số
S
2
/
S
1
bằng:A.
π...
Đọc tiếp
Cho hình lập phương có cạnh bằng a và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 là diện tích 6 mặt của hình lập phương, S 2 là diện tích xung quanh của hình trụ. Tỉ số S 2 / S 1 bằng:
A. π /6 B. 1/2
C. π /2 D. π
Cho hình lập phương ABCD.A’B’C’D’. Gọi (P) là mặt phẳng đi qua trung điểm của AC’ và vuông góc với BB’. Ảnh của tứ giác ADC’B’ qua phép đối xứng mặt phẳng (P) là: A. Tứ giác ADC’B’ B. Tứ giác A’B’C’D’ C. Tứ giác ABC’D’ D. Tứ giác A’D’CB
Đọc tiếp
Cho hình lập phương ABCD.A’B’C’D’. Gọi (P) là mặt phẳng đi qua trung điểm của AC’ và vuông góc với BB’. Ảnh của tứ giác ADC’B’ qua phép đối xứng mặt phẳng (P) là:
A. Tứ giác ADC’B’
B. Tứ giác A’B’C’D’
C. Tứ giác ABC’D’
D. Tứ giác A’D’CB
Đáp án B
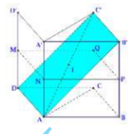
Gọi M, N, P, Q lần lượt là trung điểm của BB’, AA’, DD’, CC’
Khi đó mặt phẳng (P) thỏa yêu cầu bài toán chính là mặt phẳng (MNPQ)
Qua phép đối xứng của mặt phẳng (P) thì tứ giác ADC'B' biến thành A'D'CB
Đúng 0
Bình luận (0)