Diện tích hình phẳng giới hạn bởi các đường x=-1; x=2; y=0 và parabol  P : y = a x 2 + b x + c  bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Tính T=a+b-c

A. T = -8.   

B. T = -2.    

C. T = 14. 

D. T = 3.

Diện tích hình phẳng giới hạn bởi các đường x = − 1 ,   x = 2 ,   y = 0  và Parabol ( P ) : y = a x 2 + b x + c  bằng 15. Biết (P) có đỉnh I(1;2) là điểm cực tiểu. Khi đó a+b-c bằng bao nhiêu?

A. -8

B. -2

C. 14

D. 3

Tình diện tích hình phẳng giới hạn bởi parabol y = –x² và đường thẳng y = –x – 2.

A.  2

B.  9 2

C. 1

D.  3 4

Tính diện tích S của hình phẳng giới hạn bởi đường parabol  y = x 3 - 3 x + 2 và đường thẳng y=x-1.

A.  S = 3 4

B. S = 2

C.  S = 37 14

D.  S = 799 300

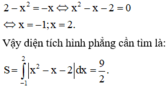
Cho (H) là hình phẳng giới hạn bởi parabol  y = 2 x 2 4  đường cong  y = 1 - x 2 4  (với  0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên).

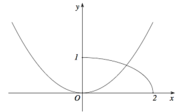
Diện tích của (H) bằng

A.  3 π - 2 12

B.  3 π + 4 2 - 6 12

C.  4 π + 3 2 - 8 12

D.  π + 2 - 2 3

Cho (H) là hình phẳng giới hạn bởi parabol y = 2 x 2 4 , đường cong  1 - x 2 4 (với 0 ≤ x ≤ 2 ) và trục hoành (tham khảo hình vẽ bên). Diện tích của (H) bằng

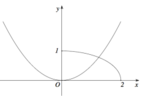
A.  3 π - 2 12

B.  3 π + 4 2 - 6 12

C.  4 π + 3 2 - 8 12

D.  π + 2 - 2 3