Gọi z1 và z2 lần lượt là hai nghiệm của phương trình z 2 - 4 z + 5 = 0 . Cho số phức w=(1+z1)(1+z2). Tìm số phức liên hợp của số phức w
A.![]() .
.
B. ![]() .
.
C.![]() .
.
D. ![]() .
.
Gọi z1, z2 lần lượt là hai nghiệm của phương trình z2 - (1 + 3i) z – 2 + 2i = 0 và thỏa mãn | z1| > | z2|. Tìm giá trị của biểu thức

A. 0,5
B. 1,5
C. 1
D. 2
Chọn B.
Phương trình đã cho tương đương với:
( z – 2i) ( z – 1 – i) = 0
Suy ra: z = 2i hoặc z = 1 + i
Do | z1| > | z2|. nên ta có z1 = 2i và z2 = 1 + i
Ta có
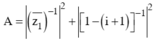
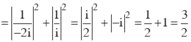
Gọi z1; z2 là hai nghiệm phức của phương trình z2 – z + 1 = 0 . Tìm phần thực, phần ảo của số phức ![]() lần lượt là?
lần lượt là?
A. 0; 1
B. 1; 0
C. -1; 0
D. 0; -1
Chọn C.
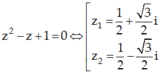
Ta có 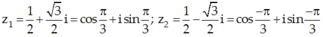
Áp dụng công thức Moa-vrơ:
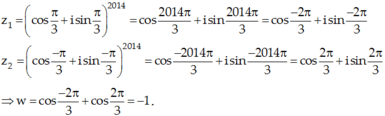
Phần thực của w là -1, phần ảo là 0.
Gọi z 1 , z 2 là hai nghiệm phức của phương trình 3 z 2 - z + 2 = 0 . Tính | z 1 | 2 + | z 2 | 2
A. -11/9
B. 8/3
C. 2/3
D. 4/3
Gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - 2z + 2 = 0, (z ∈ ℂ ). Tính giá trị của biểu thức P = 2| z 1 + z 2 | + | z 1 - z 2 |
A. P = 6
B. P = 3
C. P = 2 2 + 2
D. P = 2 + 4
Gọi z 1 , z 2 là hai nghiệm của phương trình z 2 - 2 z + 2 = 0 , z ∈ C . Tính giá trị của biểu thức P = 2 z 1 + z 2 + z 1 - z 2 .
A. P = 6
B. P = 3
C. P = 2 2 + 2
D. P = 2 + 4
Đáp án A
PT ⇔ [ z = 1 + i z = 1 - u ⇒ z 1 = 1 + i z 2 = 1 - i ⇒ z 1 + z 2 = 2 z 1 - z 2 = 2 i ⇒ z 1 + z 2 = 2 z 1 - z 2 = 2 ⇒ P = 6
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 - z + 2. Tính z 1 2 + z 2 2
A. - 11 9
B. 8 3
C. 2 3
D. 4 3
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 − z + 2 = 0. Tính z 1 2 + z 2 2
A. − 11 9
B. 8 3
C. 2 3
D. 4 3
Đáp án D
z 2 − z + 2 = 0 ⇔ z = 1 ± i 23 6 ⇒ z 1 = z 2 = 2 3
Khi đó z 1 2 + z 2 2 = 4 3
Gọi z 1 , z 2 là hai nghiệm phức của phương trình z 2 + z + 1 = 0 . Giá trị của biểu thức z 1 + z 2 bằng
A. 1 2
B. 4
C. 2
D. 1
Gọi z 1 , z 2 là 2 nghiệm của phương trình z 4 z 2 + z ¯ = − 4 ( z 2 là số phức có phần ảo âm). Khi đó z 1 + z 2 bằng:
A. 1
B. 4
C. 8
D. 2
Gọi z 1 , z 2 là 2 nghiệm của phương trình z 4 z 2 + z ¯ = - 4 ( z 2 là số phức có phần ảo âm). Khi đó z 1 + z 2 bằng
![]()
![]()
![]()
![]()