Cho hai số phức z11+3i và z23-4i. Môđun của số phức wz1/z2 là A. . B. C. . D..
Đọc tiếp
Cho hai số phức z1=1+3i và z2=3-4i. Môđun của số phức w=z1/z2 là
A. 
.
B. 
C. 
.
D.
.
Những câu hỏi liên quan
Cho hai số phức
z
1
2 + 4i và
z
2
1 - 3i. Tính môđun của số phức
z
1
+ 2i
z
2
A. |
z
1
+ 2i
z
2
| 8 B. |
z
1
+ 2i
z...
Đọc tiếp
Cho hai số phức z 1 = 2 + 4i và z 2 = 1 - 3i. Tính môđun của số phức z 1 + 2i z 2
A. | z 1 + 2i z 2 | = 8
B. | z 1 + 2i z 2 | = 10
C. | z 1 + 2i z 2 | = 1
D. | z 1 + 2i z 2 | = 10
Cho hai số phức
z
1
2
+
4
i
và
z
2
1
−
3
i
. Tính môđun của số phức
z
1
+
2
i
z
2
A.
z
1
+
2
i...
Đọc tiếp
Cho hai số phức z 1 = 2 + 4 i và z 2 = 1 − 3 i . Tính môđun của số phức z 1 + 2 i z 2
A. z 1 + 2 i z 2 = 8
B. z 1 + 2 i z 2 = 10
C. z 1 + 2 i z 2 = 1
D. z 1 + 2 i z 2 = 10
Đáp án D
Ta có:
z 1 + 2 i z 2 = 2 + 4 i + 2 i 1 − 3 i = 8 + 6 i ⇒ z 1 + 2 i z 2 = 10
Đúng 0
Bình luận (0)
Gọi
z
1
,
z
2
là hai trong số các số phức thỏa mãn
z
-
3
-
2
i
5
và
z
1
-
z
2
8
. Tìm môđun của...
Đọc tiếp
Gọi z 1 , z 2 là hai trong số các số phức thỏa mãn z - 3 - 2 i = 5 và z 1 - z 2 = 8 . Tìm môđun của số phức w = z 1 + z 2 - 6 - 4 i
A. |w| = 36
B. |w| = 10
C. |w| = 6
D. |w| = 4
Chọn đáp án C
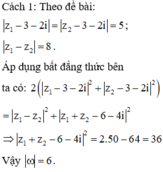
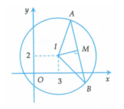
Cách 2: Gọi lần lượt là điểm biểu diễn số phức z 1 , z 2
Theo đề bài z 1 , z 2 là hai trong các số phức thỏa mãn z - 3 - 2 i = 5 nên và thuộc đường tròn tâm I(3;2), bán kính R=5.
Đúng 0
Bình luận (0)
Gọi
z
1
,
z
2
là hai trong các số phức thỏa mãn
z
-
1
+
2
i
5
và
z
1
-
z
2
8
. Tìm môđun của số...
Đọc tiếp
Gọi z 1 , z 2 là hai trong các số phức thỏa mãn z - 1 + 2 i = 5 và z 1 - z 2 = 8 . Tìm môđun của số phức w = z 1 + z 2 - 2 + 4 i ?
A. w = 6
B. w = 16
C. w = 10
D. w = 13
a) Cho hai số phức z1 = 1 + 2i ; z2 = 2 – 3i . Xác định phần thực và phần ảo của số phức z1 – 2z2 .
b) Cho hai số phức z1 = 2 + 5i ; z2 = 3 – 4i . Xác định phần thực và phần ảo của số phức z1.z2
a) Phần thực z1 – 2z2 là – 3, phần ảo của nó là 8.
b) Phần thực và phần ảo của z1.z2 tương ứng là 26 và 7.
Đúng 0
Bình luận (0)
Cho hai số phức
z
1
4
+
i
và
z
2
1
-
3
i
. Tính môđun của số phức
z
1
-
z
2
. A.
z
1
-
z
2...
Đọc tiếp
Cho hai số phức z 1 = 4 + i và z 2 = 1 - 3 i . Tính môđun của số phức z 1 - z 2 .
A. z 1 - z 2 = 17 - 10
B. z 1 - z 2 = 13
C. z 1 - z 2 = 25
D. z 1 - z 2 = 5
Đáp án D
z 1 - z 2 = 4 + i - 1 - 3 i = 3 + 4 i nên z 1 - z 2 = 5
Đúng 0
Bình luận (0)
Cho hai số phức z 1 = 1 + i và z 2 = 2 - 3 i . Môđun của số phức z 1 + z 2 bằng
A. 1
B. 5
C. 5
D. 13
Cho hai số phức
z
1
1 - i và
z
2
2 + 3i. Tính môđun của số phức
z
2
- i
z
1
A.
3
B. 5 C.
5
D.
13
Đọc tiếp
Cho hai số phức z 1 = 1 - i và z 2 = 2 + 3i. Tính môđun của số phức z 2 - i z 1
A. 3
B. 5
C. 5
D. 13
là modul của m.Cho hai số phức
z
1
1
+
i
và
z
2
2
-
3
i
. Môđun của số phức
z
z
1
-
z
2
bằng A.
17
B.
15
C.
2
+
13
D.
13...
Đọc tiếp
Cho hai số phức z 1 = 1 + i và z 2 = 2 - 3 i . Môđun của số phức z = z 1 - z 2 bằng
A. 17
B. 15
C. 2 + 13
D. 13 - 2
