Hàm số y = ax 4 + bx 2 + c có đồ thị hàm số như hình vẽ dưới đây. Mệnh đề nào sau đây đúng
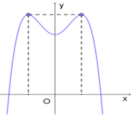
A.![]()
B. ![]()
C. ![]()
D. ![]()
Cho hàm số y=f(x)=x^3+ax^2+bx+4 có đồ thị (C) như hình vẽ. Hỏi (C) là đồ thị của hàm số y=f(x) nào?
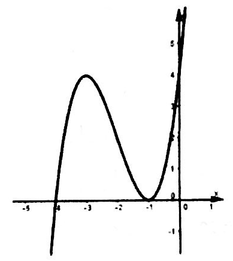
A. y = f ( x ) = x 3 - 3 x 2 + 4
B. y = f ( x ) = x 3 + 6 x 2 + 9 x + 4
C. y = f ( x ) = x 3 + 3 x 2 + 4
D. y = f ( x ) = x 3 - 6 x 2 + 9 x + 4
Cho hàm số y = a x + b x − c có đồ thị hàm số như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau:

A. a > 0 , b < 0 , c > 0
B. a > 0 , b > 0 , c < 0
C. a > 0 , b < 0 , c < 0
D. a < 0 , b > 0 , c > 0
Đáp án C
TCĐ: x = c < 0 , T C N : y = a > 0 . Đồ thị hàm số giao với trục oy tại điểm có tung độ − b c < 0 ⇒ b < 0
Đồ thị hàm số giao với trục ox tại điểm có hoành độ − b a > 0 ⇒ b < 0
Cho hàm số y = a x - b x - 1 có đồ thị như hình dưới

A. b < 0 < a
B. 0 < b < a
C. b < a < 0
D. 0 < a < b
Chọn đáp án C
Dựa vào hình vẽ ta thấy: Đồ thị có đường tiệm cận ngang là y = -1 và đường tiệm cận đứng là x = 1
Và đồ thị cắt trục hoành tại điểm có hoành độ x = 2 > 1
Suy ra
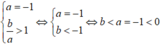
Cho đồ thị của các hàm số y = a x , y = b x , y = c x (a,b,c dương và khác 1) có đồ thị như trong hình vẽ. Chọn đáp án đúng:
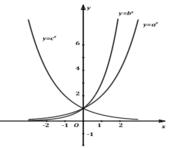
A. a > b > c
B. b > c > a
C. b > a > c
D. c > b > a
Chọn C
Đồ thị hàm số y = a x , y = b x là đồ thị của hàm số mũ cơ bản đồng biến nên a > 1; b > 1
Dựa vào đồ thị ta có :
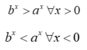
Do đó: b > a > 1
Đồ thị hàm số y = c x là đồ thị của hàm số mũ cơ bản nghịch biến nên 0 < c < 1
Vậy b > a > c
Tìm a, b để hàm số y = a x + b x + 1 có đồ thị như hình vẽ bên
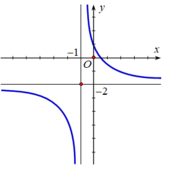
A. a = -1, b = -2
B. a = 1, b = -2
C. a = -2, b = 1
D. a = 2, b = 1
Đáp án C
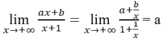
=> y = a là tiệm cận ngang.
Dựa vào đồ thị hàm số có đường thẳng y = -2 là đường tiệm cận ngang nên a = -2
Mà đồ thị hàm số đi qua điểm (0; 1) nên b = 1
Cho hàm số y = ax + b x + c có đồ thị như hình vẽ bên dưới.
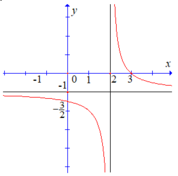
Giá trị của biểu thức a+2b+c bằng
A. -2
B. 0
C. 3
D. -1
Cho hàm số y = a x + b x − c có đồ thị như hình vẽ bên.
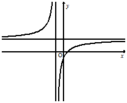
Tìm khẳng định đúng trong các khẳng định sau
A. a < 0 , b > 0 , c > 0.
B. a > 0 , b < 0 , c > 0.
C. a > 0 , b > 0 , c < 0.
D. a > 0 , b < 0 , c < 0.
Đáp án D
Đồ thị hàm số có tiệm cận ngang y = a ⇒ a > 0 .
Ta có: c<0 do đồ thị hàm số có tiệp cận đứng x=c .
Đồ thị hàm số cắt trục tung tại điểm có tung độ − b c < 0 ⇒ b < 0 .
Cho hàm số y = a x + b x - c có đồ thị như hình vẽ bên. Tìm khẳng định đúng trong các khẳng định sau
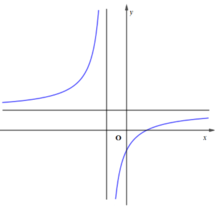
A. a > 0, b < 0, c > 0
B. a > 0, b > 0, c < 0
C. a > 0, b < 0, c < 0
D. a < 0, b > 0, c > 0
Đáp án C
Phương pháp:
Đồ thị hàm số y = a x + b c x + d có hai đường tiệm cận: x = c và y = a, đồng thời cắt trục hoành tại điểm - b a ; 0
Cách giải:
Quan sát đồ thị hàm số ta thấy: Đồ thị hàm số có tiệm cận đứng x = x0 < 0 ⇒ c < 0, đồ thị hàm số có tiệm cận ngang y = y_0 > 0 ⇒ a > 0
Đồ thị hàm số cắt trục hoành tại điểm
![]()
Cho a, b là các số thực dương khác 1. Các hàm số y = a x và y = b x có đồ thị như hình vẽ bên. Đường thẳng bất kỳ song song với trục hoành và cắt đồ thị hàm số y = a x , y = b x , trục tung lần lượt tại M, N, A đều thỏa mãn AN = 2AM. Mệnh đề nào sau đây đúng?
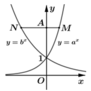
A. b = 2a
B. a 2 = b
C. a b = 1 2
D. a b 2 = 1
Gọi A(0;t) với t > 0. Suy ra 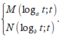
Theo giả thiết AN = 2AM nên suy ra
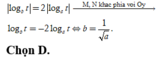
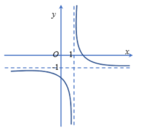
Cho hàm số y = a x + b x - 1 có đồ thị như hình vẽ. Khẳng định nào dưới đây đúng?
A. b < 0 < a
B. a < 0 < b
C. 0 < b < a
D. b < a < 0
Chọn B.
Ta có: ![]() đồ thị hàm số có tiệm cận ngang y = a
đồ thị hàm số có tiệm cận ngang y = a
Từ đồ thị hàm số ta thấy đồ thị có tiệm cận ngang y = -1 => a = -1
Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;-b) nằm bên dưới đường thẳng y = -1 nên -b < -1 ⇔ b > 1
Vậy b > 0 > a