Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 2 = y + 1 2 = z 3 ; ∆ 2 : x - 3 - 1 = y - 3 - 2 = z + 2 1
A. ∆ 1 song song với ∆ 2 .
B. ∆ 1 chéo với ∆ 2 .
C. ∆ 1 cắt ∆ 2 .
D. ∆ 1 trùng với ∆ 2 .
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 1 2 = y 1 = z + 2 - 2 , d 2 : x + 2 - 2 = y - 1 - 1 = z 2 . Xét vị trí tương đối của hai đường thẳng đã cho.
A. Chéo nhau
B. Trùng nhau
C. Song song
D. Cắt nhau
Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
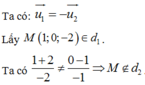
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau
Trong không gian với hệ tọa độ Oxyz, vị trí tương đối của hai đường thẳng d 1 : x = 1 + 2 t y = − 2 + 3 t z = 2 + 2 t , d 2 : x = − 1 − 2 t y = 1 + 2 t z = 3 − 3 t là
A. Song song
B. Chéo nhau
C. Cắt nhau
D. Trùng nhau
Đáp án B
Ta có
u 1 → = 2 ; 3 ; 2 , u 2 → − 2 ; 2 ; − 3 , M 1 1 ; − 2 ; 2 , M 2 − 2 ; 2 ; 3 .
u 1 → , u 2 → . M 1 M 2 → = 57 ≠ 0.
Vậy d 1 và d 2 chéo nhau.
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 1 2 = y 1 = z + 2 - 2 , d 2 : z + 2 - 2 = y - 1 - 1 = z 2 . Xét vị trị tương đối của hai đường thẳng đã cho.
A. Chéo nhau
B. Trùng nhau
C. Song song
D. Cắt nhau
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng:
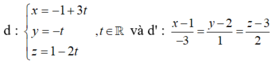
Vị trí tương đối của d và d' là:
A. song song
B. trùng nhau
C. chéo nhau
D. cắt nhau
Đáp án A
Đường thẳng d có véc-tơ chỉ phương ![]() = (3;-1;-2) và đi qua điểm M(-1;0;1).
= (3;-1;-2) và đi qua điểm M(-1;0;1).
Đường thẳng d' có véc-tơ chỉ phương ![]() =(-3;1;2).
=(-3;1;2).
Hai véc-tơ ![]() và
và ![]() cùng phương và điểm M không thuộc đường thẳng d'.
cùng phương và điểm M không thuộc đường thẳng d'.
Do đó hai đường thẳng d và d' song song với nhau.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d 1 : x = 1 y = 2 + t z = 2 − t và đường thẳng d 2 là giao tuyến của hai mặt phẳng P : x + y + z + 1 = 0 và Q : x − 2 y + z + 2 = 0 . Vị trí tương đối của hai đường thẳng d 1 , d 2 là
A. song song
B. cắt nhau.
C. chéo nhau.
D. trùng nhau.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x − 1 2 = y + 1 − 1 = z 3 và mặt phẳng ( α ) : x + 5 y + z + 4 = 0. Xác định vị trí tương đối của d và ( α )
A. d ⊥ ( α ) .
B. d ⊂ ( α ) .
C. d cắt và vuông góc với α
D. d / / ( α ) .
Trong không gian Oxyz, vị trí tương đối của hai đường thẳng :
d
1
: x = 2 + 4t, y = -6t, z = -1-8t và 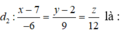
A. Cắt nhau
B. song song
C. chéo nhau
D. trùng nhau
Đáp án B
Đường thẳng d 1 đi qua điểm M 1 (2; 0; -1) và có vectơ chỉ phương là u 1 → = (4; -6; -8);
đường thẳng d 2 đi qua điểm M 2 (7; 2; 0) và có vectơ chỉ phương là u 2 → = (-6; 9; 12).
Do hai vectơ u 1 → và u 2 → cùng phương nên các đáp án A và C là sai.
Thay tọa độ điểm M 1 vào d 2 , ta thấy:
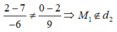
Do đó hai đường thẳng d 1 và d 2 song song.
Vậy đáp án B là đúng.
Trong không gian Oxyz cho hai đường thẳng d và d’ có phương trình lần lượt là x - 2 2 = y + 4 3 = 1 - z 2 ; x = 4 t y = - 1 + 6 t z = - 1 + 4 t . Xác định vị trí tương đối của hai đường thẳng d và d’.
A. Song song nhau
B. Trùng nhau
C. Cắt nhau
D. Chéo nhau
Đường thẳng d qua M ( 2;-4;1 ) và có vectơ chỉ phương là u → 2 ; 3 ; 2
Đường thẳng d’ qua M' ( 0;1;-1 ) và có vectơ chỉ phương là u ' → = 4 ; 6 ; 4
Do u → và u ' → cùng phương đồng thời M ∉ d ' nên hai đường thẳng đó song song nhau.
Đáp án A