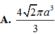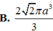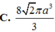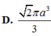Cho hình chóp S.ABC có cạnh bên SA vuông góc với mặt phẳng đáy A B C . Biết S A = a tam giác ABC là tam giác vuông cân tại A, A B = 2 a . Tính theo a thể tích V của khối chóp S.ABC.
![]()
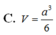
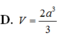
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết rằng, mặt phẳng (SBC) tạo với mặt phẳng đấy một góc 60 0 . Tính thể tích V của khối chóp S.ABC.
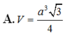
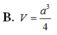
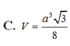
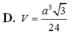
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết rằng, mặt phẳng (SBC) tạo với mặt phẳng đấy một góc 60 ° . Tính thể tích V của khối chóp S.ABC
A. V = a 3 3 4
B. V = a 3 4
C. V = a 3 3 8
D. V = a 3 3 24
Cho hình chóp S.ABC có đáy là tam giác vuông cận tại B , AB = a . Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60 0 . Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).
A. 8 2 πa 3 3
B. 4 2 πa 3 3
C. 2 2 πa 3 3
D. 2 πa 3 3
Đáp án A
Gọi M là trung điểm của AC. Tam giác ABC vuông tại B, do đó M là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi O là trung điểm của AC, suy ra OM // SA. Mà

Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Biết đường thẳng SC hợp với mặt phẳng đáy một góc 60 ° . Thể tích của khối chóp S.ABC bằng
A. a 3 4
B. a 3 2
C. a 3 8
D. 3 a 3 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, cạnh BC = a 2 , cạnh bên SA vuông góc với mặt phẳng đáy; mặt bên (SBC) tạo với mặt đáy (ABC) một góc bằng 45°. Thể tích khối chóp S.ABC theo a bằng
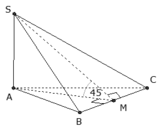
A. a 3 2 6
B. a 3 2 2
C. a 3 2 4
D. a 3 2 12
Cho hình chóp S.ABC có đáy là tam giác vuông cân cạnh bằng B, cạnh bên SA vuông góc với mặt phẳng đáy, AB=BC=a và SA=a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có đáy là tam giác vuông cân cạnh bằng B, cạnh bên SA vuông góc với mặt phẳng đáy, AB=BC=a và SA=a. Góc giữa hai mặt phẳng (SAC) và (SBC) bằng
A. 90 0 .
B. 30 0 .
C. 60 0 .
D. 45 0 .
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng a, cạnh bên SA vuông góc với đáy. Biết rằng đường thẳng SC hợp với mặt phẳng đáy một góc 60 0 . Thể tích của khối chóp S.ABC bằng
A. a 3 8
B. a 3 2
C. a 3 4
D. 3 a 3 4
Phương pháp:
Công thức tính thể tích của khối chóp có diện tích đáy S và chiều cao h là: V = 1 3 S h
Cách giải:
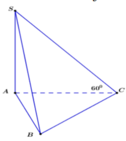

Cho hình chóp S.ABC có mặt bên SBC là tam giác đều cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy. Biết góc BAC=1200 . Bán kính mặt cầu ngoại tiếp hình chóp S.ABC là:
Gọi G là trọng tâm ABC, H là tđ BC
từ G dựng đường thẳng // SA thì nó sẽ cắt SH tại trung điểm
BK mc= SH/2 =\(\frac{\sqrt{3}}{4}\)
đúng ĐA ko
Cho hình chóp S.ABC có đáy là tam giác vuông cân tại B, AB=d. Cạnh bên SA vuông góc với mặt phẳng (ABC) và SC hợp với đáy một góc bằng 60°. Gọi (S) là mặt cầu ngoại tiếp khối chóp S.ABC. Tính thể tích khối cầu (S).