Trong không gian Oxyz cho các điểm A ( 5 ; 1 ; 5 ) , B ( 4 ; 3 ; 2 ) , C ( - 3 ; - 2 ; 1 ) . Điểm I ( a ; b ; c ) là tâm đường tròn ngoại tiếp tam giác ABC. Tính a + 2 b + c ?
A. 1
B. 3
C. 6
D. - 9
Trong không gian Oxyz, cho mặt phẳng (P): x-2y+z-5=0. Trong các điểm A(0;0;5), B(1;1;3), C(-1;2;3), D(2;1;5), có bao nhiêu điểm thuộc mặt phẳng (P)?
A. 4.
B. 3.
C. 2.
D. 1.
Trong không gian hệ tọa độ Oxyz, cho các điểm A(1;2;-1), B(3;0,-5) .Viết phương trình mặt phẳng trung trực của đoạn thẳng AB.
A. x + y - 2 z - 3 = 0
B. x - y + 2 z - 17 = 0
C. x - y - 2 z - 7 = 0
D. x + y + 2 z - 5 = 0
Trong không gian Oxyz, cho các điểm A(4;-2;4), B(-2;6;4), C(5;-1;-6). Xét các điểm M thuộc mặt phẳng (Oxy) sao cho A M B ^ = 90 ° , đoạn thẳng CD có độ dài lớn nhất bằng
A. 73
B. 5 3
C. 10
D. 8
Trong không gian Oxyz , cho điểm A(5;-2;1). Hình chiếu vuông góc của điểm A lên trục Oy là điểm
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C 0 ; 0 ; 3 , D 2 ; − 2 ; 0 . Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 điểm trong 5 điểm O, A, B, C, D?
A. 7
B. 5
C. 6
D. 10
Đáp án B
A B → ( − 1 ; 2 ; 0 ) , A D → ( 1 ; − 2 ; 0 ) , A B → = − A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10 - 1 - 6 + 2 = 5
Trong không gian tọa độ Oxyz, cho các điểm A (1;2;3), B (2;1;0), C (4;3;-2), D (3;4;1), E (1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4.
C. 5
D. Không tồn tại.
Chọn C
Ta có ![]() . Suy ra ABCD là hình bình hành.
. Suy ra ABCD là hình bình hành.
Ta lại có ![]()
E. ABCD là hình chóp đáy là hình bình hành nên các mặt phẳng cách đều 5 điểm là
+ Mặt phẳng qua 4 trung điểm của 4 cạnh bên.
+ Mặt phẳng qua 4 trung điểm lần lượt của ED, EC, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EC, EB, DC, AB.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, EB, AD, BC.
+ Mặt phẳng qua 4 trung điểm lần lượt của EA, ED, AB, DC.
Trong không gian tọa độ Oxyz, cho A(2;0;0),B(0;2;0),C(0;0;2). Có tất cả bao nhiêu điểm M trong không gian thỏa mãn M không trùng với các điểm A, B, C và A M B ^ = B M C ^ = C M A ^ = 90 o
A. 0
B. 1
C. 2
D. 3
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(1;0;0), B(0;2;0), C(0;0;3), D(2;-2;0). Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 điểm trong 5 điểm O, A, B, C, D?
A. 7
B. 5
C. 6
D. 10
Đáp án B
A B → - 1 ; 2 ; 0 , A D → 1 ; - 2 ; 0 , A B → = - A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10-1-6+2=5
Trong không gian Oxyz, cho ba điểm A(-6;0;0), B(0;-4;0), C(0;0;6). Tập hợp tất cả các điểm M trong không gian cách đều ba điểm A, B, C là một đường thẳng có phương trình là
![]()
![]()

![]()
Chọn đáp án C.
Gọi M(x;y;z) ta có
hệ điều kiện
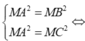
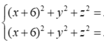
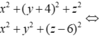
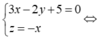
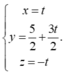
Trong không gian với hệ tọa độ Oxyz, cho các điểm:
A
1
;
0
;
0
,
B
0
;
2
;
0
,
C
0
;
0
;
3
,
D
2
;
−
2
;
0
.
Có tất cả bao nhiêu mặt phẳng phân biệt đi qua 3 trong 5 điểm O, A, B, C, D ?
A. 7
B. 5
C. 6
D. 10