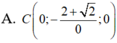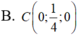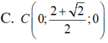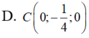Trong không gian với hệ tọa độ Oxyz, hình chiếu vuông góc của điểm A(3;2;-4) lên mặt phẳng (Oxy) có tọa độ là
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, phương trình mặt phẳng vuông góc với đường thẳng x - 2 1 = y + 2 - 2 = z 3 và đi qua điểm A ( 3 ; - 4 ; 5 ) là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz cho hai điểm A ( 2 ; 3 ; 2 ) , B ( - 2 ; - 1 ; 4 ) . Tìm tọa độ điểm E thuộc trục Oz sao cho E cách đều hai điểm A, B
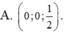
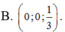
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng x = 2 + 2 t y = - 3 t z = - 3 + 5 t Phương trình chính tắc của d là
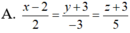
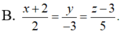
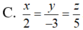
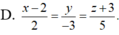
Trong không gian với hệ tọa độ Oxyz, cho hai vectơ a → = 2 ; - 3 ; 1 và b → = - 1 ; 4 ; - 2 . Giá trị của biểu thức a → . b → bằng
A. -16
B. -4
C. 4
D. 16
Trong không gian với hệ tọa độ Oxyz, đường thẳng d : x = 2 + t u = - 1 + 3 t z = 3 có một véctơ chỉ phương là
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi
qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x -y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4 = 0
Trong không gian với hệ trục tọa độ Oxyz, phương trình mặt phẳng đi qua điểm A(1;2;-3) có vectơ pháp tuyến n → = ( 2 ; - 1 ; 3 ) là
A. 2x - y + 3z + 9 = 0
B. 2x - y + 3z - 4 = 0
C. x - 2y - 4 = 0
D. 2x - y + 3z + 4
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P):x + y + z = 0 .Phương trình mặt phẳng (Q) vuông góc với (P) và cách điểm M(1;2;-1) một khoảng bằng 2 có dạng: Ax + B y + C z = 0 A 2 + B 2 + C 2 ≠ 0 . Ta có kết luận gì về giá trị của A, B, C?
A. B = 0 hay 3B + 8C = 0
B. B = 0 hay 8B + 3C = 0
C. B = 0 hay 3B - 8C = 0
D. 3B - 8C = 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;0), B(0;0;1) và mặt phẳng (P): 2x-2y-z+5=0. Tìm tọa độ điểm C trên trục Oy sao cho mặt phẳng (ABC) hợp với mặt phẳng (P) một góc 45 ° là