Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng ( α ) + x + 2 y - z - 1 = 0 và ( β ) : 2 x + 4 y - mz - 2 = 0 . Tìm m để hai mặt phẳng ( α ) và ( β ) song song với nhau.
A. m= 1.
B. Không tồn tại m.
C. m = -2.
D. m = 2.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (α): x+y+z-6=0. Điểm nào dưới đây không thuộc mặt phẳng (α)?
A. M(1; -1; 1)
B. Q(3; 3; 0)
C. N(2; 2; 2)
D. P(1; 2; 3).
Đáp án A
Ta có 1+(-1)+1-6 ≠ 0
=> Tọa độ điểm M không thỏa mãn phương trình mặt phẳng (α) nên điểm M không thuộc mặt phẳng (α).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) : x + y + z - 6 = 0 . Điểm nào dưới đây không thuộc mặt phẳng ( α ) ?
A. P(1;2;3)
B. Q(3;3;0)
C. M(1;-1;1)
D. N(2;2;2)
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng α : x + y - z + 1 = 0 v à β : - 2 x + m y + 2 z - 2 = 0 . Tìm m để mặt phẳng (α) song song với mặt phẳng (β).
A. m = 2
B. m = 5
C. Không tồn tại
D. m = -2
Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng (α): x+2y-z-1=0 và (β): 2x+4y-mz-2=0. Tìm m để hai mặt phẳng (α) và (β) song song với nhau.
A. m=1
B. Không tồn tại m
C. m=-2
D. m=2.
Đáp án B
Mặt phẳng (α) song song với mặt phẳng (β) khi và chỉ khi:
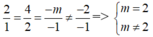
Hệ này vô nghiệm nên không có giá trị của m thỏa mãn.
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) :x+2y+3z-6=0. Hỏi điểm nào dưới đây thuộc mặt phẳng (α) ?
A. M(1;2;3).
B. N(1;1;1).
C. P(3;2;0).
D. Q(1;2;1).
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ) : x + 2 y + 3 z - 6 = 0 . Hỏi điểm nào dưới đây thuộc mặt phẳng ( α ) ?
A. M 1 ; 2 ; 3
B. N 1 ; 1 ; 1
C. P 3 ; 2 ; 0
D. Q 1 ; 2 ; 1
Trong không gian với hệ tọa độ Oxyz cho điểm M(1;4;2) và mặt phẳng ( α ) : x + y + z - 1 = 0 . Tọa độ điểm M’ đối xứng với điểm M qua mặt phẳng (α) là
A. M’(0;-2;-3)
B. M’(-3;-2;0)
C. M’(-2;0;-3)
D. M’(-3;0;-2)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng ( α ): x+y+z-6=0 . Điểm nào dưới đây không thuộc ( α ) ?
A. N(2;2;2)
B. Q(3;3;0)
C. P(1;2;3)
D. M(1;-1;1)
Đáp án D
Dễ thấy tọa độ M(1;-1;1) không thỏa mãn phương trình mặt phẳng ( α )
Trong không gian với hệ tọa độ Oxyz, cho α là mặt phẳng chứa hai đường thẳng d 1 : x − 1 3 = y + 2 − 1 = z + 1 2 và d 2 : x = 12 − 3 t y = t z = 10 − 2 t . Phương trình mặt phẳng α là
A. 15 x − 11 y − 17 z − 54 = 0 .
B. 15 x + 11 y − 17 z + 10 = 0 .
C. 15 x − 11 y − 17 z − 24 = 0.
D. 15 x + 11 y − 17 z − 10 = 0 .
Đáp án D
Đường thẳng d 1 đi qua M 1 1 ; − 2 ; − 1 và có VTCP u 1 → = 3 ; − 1 ; 2 .
Đường thẳng d 2 đi qua M 2 12 ; 0 ; 10 và có VTCP u 2 → = − 3 ; 1 ; − 2 .
Như vậy: u 1 → = − u 2 → , M 1 ∉ d 2 . Suy ra d 1 / / d 2 .
Chú ý: Hai đường thẳng d 1 và d 2 song song nên em không thể lấy tích có hướng của hai VTCP để tìm VTPT của mặt phẳng vì tích có hướng của hai vectơ cùng phương là vectơ-không.
Gọi n → là một VTPT của mặt phẳng α thì vuông n → góc với hai vectơ không cùng phương
