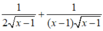Đạo hàm của hàm số y = - x 2 + 3 x - 3 2 ( x - 1 ) bằng biểu thức có dạng ax 2 + bx 2 ( x - 1 ) 2 . Khi đó a.b bằng
A. -1 .
B. 6 .
C. 4 .
D. -2 .
Những câu hỏi liên quan
Tính đạo hàm của hàm số sau y = (x2 + 3x)(2 – x).
A: -3x2 – 2x + 6
B: -3x2 + 2x + 6
C: -3x2 – 2x – 6
D: 3x2 – 2x + 6
Chọn A.
y’ = ((x2 + 3x)(2 – x))’ = (x2 + 3x)’.(2 – x) + (x2 + 3x).(2 – x)’
= (2x + 3)(2 – x) + (x2 + 3x)(-1) = -3x2 – 2x + 6.
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau:
y
2
-
x
2
3
-
x
3
1
-
x
+
x...
Đọc tiếp
Tính đạo hàm của hàm số sau: y = 2 - x 2 3 - x 3 1 - x + x 2
A.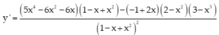 
B.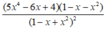 
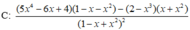
D: Tất cả sai.
Tính đạo hàm của hàm số sau y = x(2x - 1)(3x + 2)
A: 18x2 + 2x + 2
B: 18x2 + 2x - 2
C: 9x2 + 2x - 2
D: 2x - 2
Chọn B.
Ta có: y = (2x – 1)(3x + 2) = (2x2 – x)(3x + 2)
y’ = [(2x2 – x)(3x + 2)]’ = (2x2 – x)’(3x + 2) + (3x + 2)’.(2x2 – x)
= (4x – 1)(3x + 2) + 3(2x2 – x) = 18x2 + 2x – 2.
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau:
y
x
+
x
+
x
A. B.
1
2
x
x
x
1
+
1
2...
Đọc tiếp
Tính đạo hàm của hàm số sau: y = x + x + x
A. 
B. 1 2 x x x 1 + 1 2 x
C.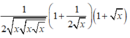 
D. 1 2 x x x 1 + 1 2 x 1 + x
Tính đạo hàm của hàm số sau:
y
x
-
1
x
5
A. 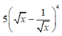B. 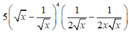C. 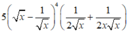D: Tất cả sai
Đọc tiếp
Tính đạo hàm của hàm số sau: y = x - 1 x 5
A. 
B. 
C. 
D: Tất cả sai
Tính đạo hàm của hàm số sau
y
3
x
2
-
x
Đọc tiếp
Tính đạo hàm của hàm số sau y = 3 x 2 - x
Tính đạo hàm của hàm số sau: y (x2 – x + 1)3.(x2 + x + 1)2 A: (x2 – x + 1)2(x2 + x + 1) B: (x2 – x + 1)2(x2 + x + 1)[(2x + 3)(x + x2)] C: (x2 – x + 1)2(x2 + x + 1)[3(2x - 1) + 2(2x + 1)] D: Tất cả sai
Đọc tiếp
Tính đạo hàm của hàm số sau: y = (x2 – x + 1)3.(x2 + x + 1)2
A: (x2 – x + 1)2(x2 + x + 1)
B: (x2 – x + 1)2(x2 + x + 1)[(2x + 3)(x + x2)]
C: (x2 – x + 1)2(x2 + x + 1)[3(2x - 1) + 2(2x + 1)]
D: Tất cả sai
Chọn D.
Đầu tiên sử dụng quy tắc nhân.
y’ = [(x2 – x + 1)]’(x2 + x + 1)2 + [(x2 x + 1)2]/(x2 – x + 1)3.
Sau đó sử dụng công thức u a '
y' = 3(x2 – x + 1)2(x2 – x + 1)’(x2 + x + 1) + 2(x2 + x + 1)(x2 + x + 1)’(x2 – x + 1)3
y’ = 3(x2 – x + 1)2(2x – 1) (x2 + x + 1)2 + 2(x2 + x + 1)(2x + 1)(x2 – x + 1)3
y’ = (x2 – x + 1)2(x2 + x + 1)[3(2x – 1)(x2 + x + 1) + 2(2x + 1)(x2 – x + 1)].
Đúng 0
Bình luận (0)
Tính đạo hàm của hàm số sau:
y
1
x
2
-
x
+
1
5
A. B. C. D: Tất cả sai
Đọc tiếp
Tính đạo hàm của hàm số sau: y = 1 x 2 - x + 1 5
A. 
B.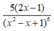 
C.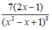 
D: Tất cả sai
Tính đạo hàm của hàm số sau
y
1
+
x
-
x
2
1
-
x
+
x
2
A. 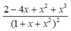B. 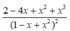C. 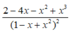D.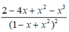
Đọc tiếp
Tính đạo hàm của hàm số sau y = 1 + x - x 2 1 - x + x 2
A. 
B. 
C. 
D. 
Tính đạo hàm của hàm số sau:
y
x
-
1
+
1
x
-
1
A. B. C. D.
Đọc tiếp
Tính đạo hàm của hàm số sau: y = x - 1 + 1 x - 1
A.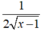 
B.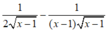 
C.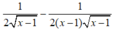 
D. 
