Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 1 2 = y 1 = z + 2 - 2 , d 2 : z + 2 - 2 = y - 1 - 1 = z 2 . Xét vị trị tương đối của hai đường thẳng đã cho.
A. Chéo nhau
B. Trùng nhau
C. Song song
D. Cắt nhau
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
d
:
x
1
+
t
y
2
+
3
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d : x = 1 + t y = 2 + 3 t z = 3 - t , d ' : x = 2 - 2 t ' y = - 2 + t ' z = 1 + 3 t ' . Tìm tọa độ giao điểm M của hai đường thẳng d và d’
A. M(-1;0;4)
B. M(4;0;-1)
C. M(0;4;-1)
D. M(0;-1;4)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d:
x
1
+
t
y
2
+
3
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d: x = 1 + t y = 2 + 3 t z = 3 - t và d': x = 2 - 2 t ' y = - 2 - t ' z = 1 + 3 t ' . Tìm tọa độ M giao điểm của d và d'.
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
t
y
1
z
-
1
-
2
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x = t y = 1 z = - 1 - 2 t . Điểm N’ đối xứng với điểm N(0;2;4) qua đường thẳng d có tọa độ là:
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng
∆
cắt hai đường thẳng
d
:
x
t
y
-
4
+
t
z...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng ∆ cắt hai đường thẳng d : x = t y = - 4 + t z = - 13 + 2 t , d ' : x = - 7 + 3 t ' y = - 1 - 2 t ' z = 8 và vuông góc với mặt phẳng tọa độ (Oxz) là:
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng
∆
cắt hai đường thẳng
d
:
x
t
y
-
4
+
t
z...
Đọc tiếp
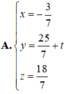
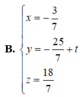
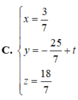
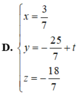
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng ∆ cắt hai đường thẳng d : x = t y = - 4 + t z = - 13 + 2 t , d ' : x = - 7 + 3 t ' y = - 1 - 2 t ' z = 8 và vuông góc với mặt phẳng tọa độ (Oxz) là:
A. x = - 3 7 y = 25 7 + t z = 18 7
B. x = - 3 7 y = - 25 7 + t z = 18 7
C. x = 3 7 y = - 25 7 + t z = 18 7
D. x = 3 7 y = - 25 7 + t z = - 18 7
Chọn C
Gọi tọa độ giao điểm của đường thẳng ∆ và hai đường thẳng d và d’ lần lượt là A t ; - 4 + t ; - 13 + 2 t ; B - 7 + 3 t ' ; - 1 - 2 t ' ; 8 Tìm t và t’ từ điều kiện A B → cùng phương với véc tơ J → = 0 ; 1 ; 0 là véc tơ pháp tuyến của (oxz)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
2
2
y
-
1
-
1
z
-
3
3
. Đường thẳng d đi qua điểm M và có vectơ chỉ phương
α
d
→
có tọa độ là: A. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương α d → có tọa độ là:
A. M 2 ; - 1 ; 3 , α d → = - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , α d → = 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , α d → = 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , α d → = 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương 
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
2
2
y
-
1
-
1
z
-
3
3
. Đường thẳng d đi qua điểm M và có vectơ chỉ phương
α
d
→
có tọa độ là: A. ...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương α d → có tọa độ là:
A. M 2 ; - 1 ; 3 , α d → = - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , α d → = 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , α d → = 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , α d → = 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương 
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng
d
:
x
+
2
2
y
-
1
-
1
z
-
3
3
. Đường thẳng d đi qua điểm M và có vectơ chỉ phương
u
→
có tọa độ là: A.
M
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d : x + 2 2 = y - 1 - 1 = z - 3 3 . Đường thẳng d đi qua điểm M và có vectơ chỉ phương u → có tọa độ là:
A. M 2 ; - 1 ; 3 , u → - 2 ; 1 ; 3
B. M 2 ; - 1 ; - 3 , u → 2 ; - 1 ; 3
C. M - 2 ; 1 ; 3 , u → 2 ; - 1 ; 3
D. M 2 ; - 1 ; 3 , u → 2 ; - 1 ; - 3
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương u → 2 ; - 1 ; 3 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d:
x
-
3
2
y
+
2
-
1
z
+
1
4
. Điểm nào sau đây không thuộc đường thẳng
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x - 3 2 = y + 2 - 1 = z + 1 4 . Điểm nào sau đây không thuộc đường thẳng
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
1
y
-
2
z
+
1
1
và
d
:
x
-
1
-
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x 1 = y - 2 = z + 1 1 và d ' : x - 1 - 2 = y - 2 4 = z 2 . Viết phương trình mặt phẳn (Q) chứa hai đường thẳng d và d’.
Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
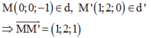
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
Phương trình mặt phẳng
Đúng 0
Bình luận (0)