Trong không gian Oxyz, cho hai đường thẳng △ : x + 3 1 = y - 1 1 = z + 2 4 và mặt phẳng (P): x+y-2z+6=0. Biết △ cắt mặt phẳng (P) tại A, M thuộc △ sao cho A M = 2 3 . Tính khoảng cách từ M tới mặt phẳng (P).
A. 2
B. 2
C. 3
D. 3
Trong không gian Oxyz, cho mặt phẳng Oxyz và hai đường thẳng d 1 : x + 1 - 1 = y - 6 2 = z 1 và d 2 : x - 1 - 3 = y - 2 - 1 = z + 4 4 Đường thẳng vuông góc với (P) và cắt cả hai đường thẳng d 1 và d 2 có phương trình là
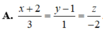
![]()
![]()
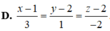
Trong không gian Oxyz, cho hai đường thẳng chéo nhau d 1 : x - 1 3 = y + 1 2 = z - 2 - 2 , d 2 : x - 4 2 = y - 4 2 = z + 3 - 1 . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là
A. x - 4 2 = y + 1 - 1 = z 2
B. x - 2 6 = y - 2 3 = z + 2 - 2
C. x - 2 2 = y - 2 - 1 = z + 2 2
D. x - 4 2 = y - 1 - 1 = z 2
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y - 3 - 1 = z + 1 1 và d 2 : x - 3 2 = y - 1 - 2 = z - m 1 Có bao nhiêu số thực m để hai đường thẳng d1, d2 cắt nhau?
A. 2
B. 0
C. 1
D. Vô số
Đường thẳng d1 qua điểm ![]() đường thẳng d2 qua điểm
đường thẳng d2 qua điểm ![]() Ta có
Ta có ![]() chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
chéo nhau hoặc cắt nhau. Để d1, d2 cắt nhau điều kiện là
![]()
![]()
![]() (luôn đúng).
(luôn đúng).
Vậy với mọi m hai đường thẳng đã cho luôn cắt nhau.
Chọn đáp án D.
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 1 - 2 = y + 2 1 = z - 3 2 và △ 2 : x + 3 1 = y - 1 1 = z + 2 - 4 . Góc giữa hai đường thẳng △ 1 , △ 2 bằng
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 3 - 1 ; d 2 : x 1 = y - 1 2 = z - 6 3 chéo nhau. Đường vuông góc chung của hai đường thẳng d 1 , d 2 có phương trình là
A. x - 1 5 = y + 2 - 4 = z - 3 1
B. x - 1 5 = y + 1 - 4 = z - 1 1
C. x + 1 5 = y + 1 - 4 = z - 3 1
D. x + 1 3 = y + 1 - 2 = z - 3 1
Đáp án C
![]()
![]()
![]()
Theo giả thiết ta giải hệ điều kiện :
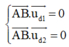
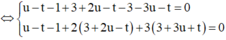
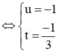
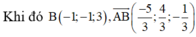
![]()
Vậy PT đường vuông góc chung là AB: x + 1 5 = y + 1 - 4 = z - 3 1
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 1 = y + 2 1 = z - 3 - 1 ; d 2 : x 1 = y - 1 2 = z - 6 3 chéo nhau. Đường vuông góc chung của hai đường thẳng d 1 ; d 2 có phương trình là
A. x - 1 5 = y + 2 - 4 = z - 3 1
B. x - 1 5 = y + 1 - 4 = z - 1 1
C. x + 1 5 = y + 1 - 4 = z - 3 1
D. x + 1 3 = y + 1 - 2 = z - 3 1
Trong không gian Oxyz, cho điểm A(1;-1;1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 . Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng ∆ , ∆ ' là:
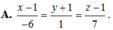
![]()
![]()
![]()
Trong không gian Oxyz , cho hai đường thẳng d1: x - 1 2 = y + 2 - 1 = z 1 và d2: x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t
Khoảng cách giữa hai đường thẳng đã cho bằng
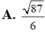
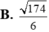
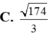
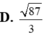
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 .
Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:
![]()
![]()
![]()
![]()
Chọn C
Gọi d là đường thẳng cần tìm.

Đường thẳng cần tìm qua A và nhận ![]() là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình:
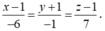
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng cắt nhau d 1 : x - 1 2 = y + 1 1 = z - 1 , d 2 : x - 3 - 1 = y 2 = z + 1 1 . Viết phương trình mặt phẳng chứa hai đường thẳng d 1 , d 2 .
A. 3x-y+5z-4=0.
B. 3x-y+5z+4=0.
C. 3x-y-5z-4=0.
D. 3x-y-5z+4=0.