Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, A B = B C = 3 a 2 , S A B ^ = S C B ^ = 90 ∘ . Biết khoảng cách từ A đến mặt phẳng (SCB) bằng 2 a 3 . Tính thể tích mặt cầu ngoại tiếp hình chóp S.ABC.
Những câu hỏi liên quan
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB BC a cạnh bên SA vuông góc với đáy và SA a. Tính diện tích toàn phần
S
t
p
của hình chóp S.ABC. A.
S
t
p
2
a
2
B.
S
t
p
a...
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, AB = BC = a cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
A. S t p = 2 a 2
B. S t p = a 2 1 + 2
C. S t p = a 2 1 + 2 2
D. S t p = 2 a 2 2
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B,
A
B
B
C
a
, cạnh bên SA vuông góc với đáy và SA a. Tính diện tích toàn phần
S
t
p
của hình chóp S.ABC.
Đọc tiếp
Cho hình chóp tam giác S.ABC có đáy ABC là tam giác vuông cân tại B, A B = B C = a , cạnh bên SA vuông góc với đáy và SA = a. Tính diện tích toàn phần S t p của hình chóp S.ABC.
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450. A.
a
3
3
4
B.
a
3
3...
Đọc tiếp
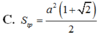
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450.
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Đáp án C
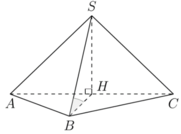
Gọi H là trung điểm AC. Ta có tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với (ABC)
suy ra S H ⊥ A B C
Ta có
S B , A B C = S B H ^ = 45 o ⇒ S H = B H = 1 2 A C = a 2 2 V S . A B C = 1 3 . a 2 2 . 1 2 a 2 = a 3 2 12
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450 A.
a
3
3
4
B.
a
3
3
12...
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, AB = a, tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với đáy. Tính thể tích khối chóp S.ABC biết góc giữa SB và mặt phẳng (ABC) bằng 450
A. a 3 3 4
B. a 3 3 12
C. a 3 2 12
D. a 3 2 4
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B có AB=BC=a,SB=2a và SA vuông góc với đáy. Tính thể tích khối chóp S.ABC.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B,
A
B
a
, cạnh bên SA vuông góc với mặt đáy,
S
A
a
. Thể tích khối chóp S.ABC bằng A.
a
3
6
B.
a
3
6
C.
6
a
3
D....
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, A B = a , cạnh bên SA vuông góc với mặt đáy, S A = a . Thể tích khối chóp S.ABC bằng
A. a 3 6
B. a 3 6
C. 6 a 3
D. 6 a 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB a, cạnh bên SA vuông góc với mặt đáy, SA a. Thể tích khối chóp S.ABC bằng
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB = a, cạnh bên SA vuông góc với mặt đáy, SA = a. Thể tích khối chóp S.ABC bằng
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B,
A
B
a
;
S
A
2
a
;
S
A
⊥
A
B
C
. Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC là: A.
a
6
2
...
Đọc tiếp
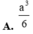
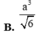
Cho hình chóp S.ABC có đáy là tam giác ABC vuông cân tại B, A B = a ; S A = 2 a ; S A ⊥ A B C . Bán kính của mặt cầu ngoại tiếp hình chóp S.ABC là:
A. a 6 2
B. a 6 6
C. a 3 2
D. a 6 3
Gọi O, I lần lượt là trung điểm của AC, SC.
Ta có:
∆ A B C vuông cân tại B ⇒ O là tâm đường tròn ngoại tiếp và A C = A B 2 = a 2 .
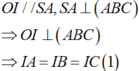
∆ S A C vuông tại A, I là trung điểm của S C ⇒ I S = I C = I A 2
Từ (1), (2) suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính
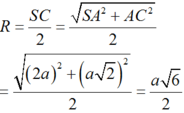
Chọn: A
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B. Có cạnh AB a. Góc giữa SB và mặt đáy là
60
o
. Thể tích hình chóp là: A.
a
3
3
3
B.
a
3
3...
Đọc tiếp
Cho hình chóp tam giác S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B. Có cạnh AB = a. Góc giữa SB và mặt đáy là 60 o . Thể tích hình chóp là:
A. a 3 3 3
B. a 3 3 4
C. a 3 3 5
D. a 3 3 6
Đáp án D
Có S A B C = 1 2 . a . a = a 2 2
Vậy V S . A B C = 1 3 S A . S A B C = a 3 3 6
Đúng 0
Bình luận (0)
Cho hình chóp tam giác S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B. Có cạnh ABa. Góc giữa SB và mặt đáy là
60
°
. Thể tích hình chóp là: A.
a
3
3
3
B.
a
3
3
4
C.
a...
Đọc tiếp
Cho hình chóp tam giác S.ABC có SA vuông góc với đáy, tam giác ABC vuông cân tại B. Có cạnh AB=a. Góc giữa SB và mặt đáy là 60 ° . Thể tích hình chóp là:
A. a 3 3 3
B. a 3 3 4
C. a 3 3 5
D. a 3 3 6
