Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB. Mặt phẳng (AA'C'C) tạo với đáy một góc bằng 45°. Tính thể tích V của khối lăng trụ ABC.A'B'C'?
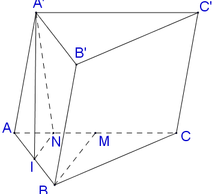
Gọi H, M, I lần lượt là trung điểm của các đoạn thẳng AB, AC, AM.
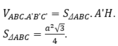
Ta có IH là đường trung bình của tam giác AMB, MB là trung tuyến của tam giác đều ABC.
Do đó:
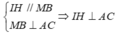
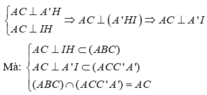
⇒ A ' I H ^ là góc gữa hai mặt phẳng (AA'C'C) và (ABCD)
⇒ A ' I H ^ = 45 °
Trong tam giác A'HI vuông tại H, ta có:

Đúng 0
Bình luận (0)
ho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng 45°. Hình chiếu vuông góc của A’ trên (ABC) là trung điểm của AB. Mặt phẳng (AA'C'C) tạo với đáy một góc bằng 45°. Tính thể tích V của khối lăng trụ ABC.A'B'C'.
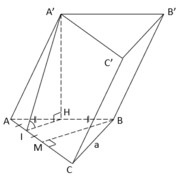
Gọi H, M, I lần lượt là trung điểm của các đoạn thẳng AB, AC, AM.

Ta có IH là đường trung bình của tam giác AMB, MB là trung tuyến của tam giác đều ABC.
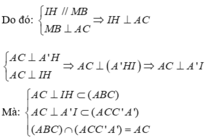
![]()
![]()
Trong tam giác A'HI vuông tại H, ta có:
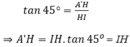
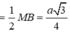
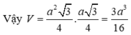
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích khối lăng trụ bằng: A.
V
3
a
3
32
B.
V
3
a
3...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích khối lăng trụ bằng:
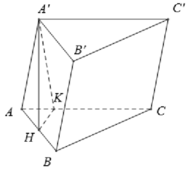
A. V = 3 a 3 32
B. V = 3 a 3 16
C. V = 3 a 3 4
D. V = 3 a 3 8
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích của khối lăng trụ ABC.A’B’C’ bằng: A.
a
3
2
B.
3
a
3
4
C....
Đọc tiếp
Cho hình lăng trụ ABC.A’B’C’ có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A’ xuống mặt phẳng (ABC) là trung điểm của AB. Mặt bên (AA’C’C) tạo với đáy một góc bằng 45°. Thể tích của khối lăng trụ ABC.A’B’C’ bằng:

A. a 3 2
B. 3 a 3 4
C. 3 a 3 16
D. 3 a 3 2
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACCA) tạo với đáy một góc
60
0
. Tính thể tích khối lăng trụ ABC.ABC. A.
a
3
3
3
B.
3...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A' xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC'A') tạo với đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A'B'C'.
A. a 3 3 3
B. 3 a 3 3 3
C. 3 a 3 2
D. a 3 3 2
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc
60
0
. Tính thể tích khối lăng trụ ABC.A′B′C′. A.
3
a
3
2
B.
3
a...
Đọc tiếp
Cho hình lăng trụ ABC.A′B′C′ có đáy ABC là tam giác đều cạnh 2a. Hình chiếu vuông góc của A′ xuống mặt phẳng ABC trùng với trung điểm của cạnh AB. Mặt bên (ACC′A′) tạo với đáy một góc 60 0 . Tính thể tích khối lăng trụ ABC.A′B′C′.
A. 3 a 3 2
B. 3 a 3 3 2
C. a 3 3 2
D. a 3 3 3
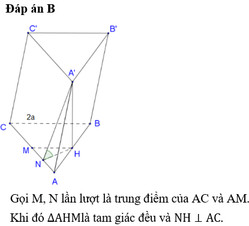
Đáp án B
Gọi M, N lần lượt là trung điểm của AC và AM.
Khi đó ΔAHM là tam giác đều và NH ⊥ AC .


Đúng 0
Bình luận (0)
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 300. Tính thể tích của lăng trụ đã cho theo a. A. 3a3/4 B. a3/4 C. a3/24 D. a3/8
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh bằng a. Hình chiếu vuông góc của A' trên mặt phẳng (ABC) trùng với trung điểm H của cạnh AB. Góc giữa cạnh bên của lăng trụ và mặt đáy bằng 300. Tính thể tích của lăng trụ đã cho theo a.
A. 3a3/4
B. a3/4
C. a3/24
D. a3/8
Đáp án D
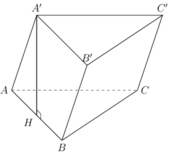
Ta có góc giữa cạnh bên AA' với mặt đáy (ABC) là:
góc A ' A H ^ và tan A ' A H = A ' H A H
Suy ra A ' H = a 2 . tan 30 ° = a 3 6
Do đó V = A ' H . S A B C = a 3 6 . a 2 3 4 = a 3 8
Đúng 0
Bình luận (0)
Cho hình lăng trụ MNP. M’N’P’ có đáy MNP là tam giác đều cạnh bằng a, hình chiếu vuông góc của M’ xuống mặt phẳng ( MNP ) là trung điểm của MN. Mặt bên (MM’N’P’) tạo với đáy một góc bằng 45độ, tính thể tích của khối lăng trụ này
Xem chi tiết
Cho lăng trụ
A
B
C
.
A
B
C
có đáy ABC là tam giác đều cạn a. Hình chiếu vuông góc của A xuống mặt (ABC) là trung điểm của AB. Mặt bên
A
C
C
A
tạo với đáy góc
45
°
. Thể tích khối lăng trụ này theo a là A. ...
Đọc tiếp
Cho lăng trụ A B C . A ' B ' C ' có đáy ABC là tam giác đều cạn a. Hình chiếu vuông góc của A' xuống mặt (ABC) là trung điểm của AB. Mặt bên A C C ' A ' tạo với đáy góc 45 ° . Thể tích khối lăng trụ này theo a là
A. 3 a 3 16
B. a 3 3 3
C. 2 a 3 3 3
D. a 3 16
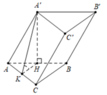
Đáp án A
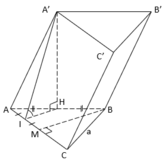
Gọi H là trung điểm của A B ⇒ A ' H ⊥ A B C
Kẻ H K ⊥ A C K ∈ A C và A ' H ⊥ A C ⇒ A C ⊥ A ' H K
Suy ra A C C ' A ' ; A B C ^ = A ' K ; H K ^ = A ' K H ^ = 45 0
Tam giác A ' H K VUÔNG TẠI H , CÓ A ' K H ^ = 45 0 ⇒ A ' H = a 3 4
Vậy thể tích khối lăng trụ là V = A ' H . S Δ A B C = a 3 4 . a 2 3 4 = 3 a 2 16
Đúng 0
Bình luận (0)
Cho hình lăng trụ ABC.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A xuống (ABC) là trung điểm của AB. Mặt bên (ACCA) tạo với đáy góc
45
0
. Thể tích khối lăng trụ ABCD.ABCD là A.
a
3
24
B.
a
3
16
C.
a
3...
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A' xuống (ABC) là trung điểm của AB. Mặt bên (ACC'A') tạo với đáy góc 45 0 . Thể tích khối lăng trụ ABCD.A'B'C'D' là
A. a 3 24
B. a 3 16
C. a 3 8
D. a 3 12