Trong không gian Oxyz, cho hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2 . Mệnh đề nào dưới đây đúng?
A. ∆ 1 v à ∆ 2 trùng nhau
B. ∆ 1 v à ∆ 2 song song
C. ∆ 1 v à ∆ 2 chéo nhau
D. ∆ 1 v à ∆ 2 cắt nhau
Trong không gian Oxyz cho hai đường thẳng: d 1 : x = 1 - t y = t z = - 1 d 2 : x = 2 t ' y = - 1 + t ' z = t '
Chứng minh rằng hai đường thẳng d 1 v à d 2 chéo nhau
Trong không gian Oxyz, cho mặt phẳng Oxyz và hai đường thẳng d 1 : x + 1 - 1 = y - 6 2 = z 1 và d 2 : x - 1 - 3 = y - 2 - 1 = z + 4 4 Đường thẳng vuông góc với (P) và cắt cả hai đường thẳng d 1 và d 2 có phương trình là
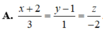
![]()
![]()
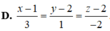
Trong không gian Oxyz , cho hai đường thẳng d1: x - 1 2 = y + 2 - 1 = z 1 và d2: x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t
Khoảng cách giữa hai đường thẳng đã cho bằng
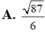
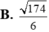
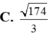
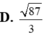
Trong không gian Oxyz, cho hai đường thẳng d 1 : x = - 1 + t y = 3 + 2 t z = - 1 - t
và d 2 : x = 7 + 3 s y = 1 - s z = 5 - s .Khoảng cách giữa hai đường thẳng đã cho bằng
A. 31
B. 6 2
C. 62
D. 4 2
Trong không gian Oxyz cho hai đường thẳng có phương trình x = 1 + 2 t y = − 1 − t z = 1 và x = 2 − t y = − 2 − t z = 3 + t .Tìm khoảng cách giừa hai đường thẳng
A. 6
B. 3 6
C. 6 2
D. 3 6 2
Trong không gian Oxyz cho hai đường thẳng có phương trình x = 1 + 2 t y = − 1 − t z = 1 và x = 2 − t y = − 2 − t z = 3 + t .Tìm khoảng cách giừa hai đường thẳng.
A. 6
B. 3 6
C. 6 2
D. 3 6 2
Đáp án C
Đường thẳng Δ : x = 1 + 2 t y = − 1 − t z = 1 đi qua điểm A 1 ; − 1 ; 1 và có vtcp u → = 2 ; − 1 ; 0
Đường thẳng Δ ' : x = 2 − t y = − 2 + t z = 3 + t đi qua điểm B 2 ; − 2 ; 3 và có vtcp u ' → = − 1 ; 1 ; 1
Vậy d Δ , Δ ' = u → , u ' → . A B → u → , u ' →

u → , u ' → = − 1 ; − 2 ; 1 ⇒ u → , u ' → = 6 ; A B → = 1 ; − 1 ; 2 ⇒ d Δ , Δ ' = 3 6 = 6 2
Trong không gian Oxyz, cho hai đường thẳng △ 1 : x - 1 - 2 = y + 2 1 = z - 3 2 và △ 2 : x + 3 1 = y - 1 1 = z + 2 - 4 . Góc giữa hai đường thẳng △ 1 , △ 2 bằng
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Trong không gian Oxyz, cho hai đường thẳng d 1 : x - 1 2 = y + 2 - 1 = z 1 và d 2 : x = 1 + 4 t y = - 1 - 2 t z = 2 + 2 t , t ∈ R . Khoảng cách giữa hai đường thẳng đã cho bằng
A. 87 6
B. 174 6
C. 174 3
D. 87 3
Trong không gian Oxyz, cho điểm A (1; -1; 1) và hai đường thẳng ∆ : x - 1 2 = y 1 = z - 3 - 1 , ∆ ' : x 1 = y + 1 - 2 = z - 2 1 .
Phương trình đường thẳng đi qua điểm A và cắt cả hai đường thẳng Δ, Δ' là:
![]()
![]()
![]()
![]()
Chọn C
Gọi d là đường thẳng cần tìm.

Đường thẳng cần tìm qua A và nhận ![]() là véc tơ chỉ phương nên có phương trình:
là véc tơ chỉ phương nên có phương trình:
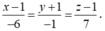
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 2 1 = y - 1 - 1 = z - 2 - 1 và d 2 : x = t y = 3 z = - 2 + t . Phương trình đường vuông góc chung của hai đường thẳng d 1 , d 2 là.
A. x = 2 + t y = 1 + 2 t z = 2 - t
B. x = 3 + t y = 3 - 2 t z = 1 - t
C. x = 2 + 3 t y = 1 - 2 t z = 2 - 5 t
D. x = 3 + t y = 3 z = 1 - t
Chọn A.
Gọi d là đường thẳng cần tìm

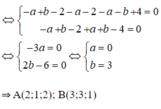
d đi qua điểm A(2;1;2) và có vectơ chỉ phương ![]()
