Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A 0 ; - 1 ; 1 , B ( - 2 ; 1 ; - 1 ) và C - 1 ; 3 ; 2 . Biết rằng ABCD là hình bình hành. Khi đó tọa độ điểm D là
A. D - 1 ; 1 ; 2 3
B. D 1 ; 3 ; 4
C. D 1 ; 1 ; 4
D. D - 1 ; - 3 ; - 2
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): x - y + z + 3 = 0 và ba điểm A(0;1;2), B(1;1;1), C(2;-2;3) Tọa độ điểm M thuộc (P) sao cho M A → + M B → + M C → nhỏ nhất là
A. M(0;0;−3)
B. M(1;1;−3)
C. M(−1;2;0)
D. M(2;1;−1)
Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
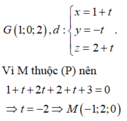
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x − y + z + 3 = 0 và ba điểm A 0 ; 1 ; 2 , B 1 ; 1 ; 1 , C 2 ; − 2 ; 3 . Tọa độ điểm M thuộc (P) sao cho MA → + MB → + MC → nhỏ nhất là
A. M − 1 ; 2 ; 0
B. M 1 ; 1 ; − 3
C. M 0 ; 0 ; − 3
D. M 2 ; 1 ; − 1
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng P : x - y + z + 3 = 0 và ba điểm A 0 ; 1 ; 2 , B 1 ; 1 ; 1 , C 2 ; - 2 ; 3 . Tọa độ điểm M thuộc (P) sao cho M A → + M B → + M C → nhỏ nhất là
A. M(0;0;-3)
B. M(1;1;-3)
C. M(-1;2;0)
D. M(2;1;-1)
Đáp án C
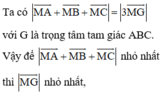
hay M là hình chiếu của G lên mặt phẳng (P).
Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
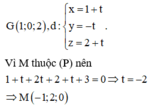
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M → = 2 A B → - A C →
A. M (-2;6;-4)
B. M (2;-6;4)
C. M (-2;-6;4)
D. M (5;5;0)
Chọn C.
Phương pháp: Hai véc tơ bằng nhau khi và chỉ khi các tọa độ tương ứng bằng nhau.

Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A (3;2;l), B (l;-1;2), C (l;2;-1). Tìm tọa độ điểm M thỏa mãn O M ⇀ = 2 A B ⇀ - A C ⇀
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, gọi (α) là mặt phẳng cắt ba trục tọa độ tại ba điểm A(2;0;0), B(0;3;0), C(0;0;1) Phương trình của α là
![]()
![]()
![]()
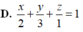
Trong không gian với hệ trục tọa độ Oxyz, cho véc-tơ ![]() . Tìm tọa độ điểm A.
. Tìm tọa độ điểm A.
A. A(-2;3;0)
B. A(-2;0;3)
C. A(0;2;-3)
D. A(0;-2;3).